1. 공분산이란?
공분산은 통계적으로 두 변수 간의 관계를 측정하는 지표로, 두 변수가 함께 어떻게 변하는지를 나타냅니다. 이것은 데이터 분석 및 통계 모델링에서 중요한 역할을 합니다.
2023.10.23 - [전체글] - [통계공부] 2. 평균, 편차, 분산, 표준편차
[통계공부] 2.평균, 편차, 분산, 표준편차
1. 평균 (Mean) 평균은 데이터 집합의 중심 위치를 나타내는 통계적 지표로, 모든 데이터 포인트의 합을 데이터의 개수로 나눈 값입니다. 이것은 데이터의 대표값 중 하나로, 집단의 전반적인 경향
informyun.com
2. 공분산의 기본 공식 및 해석
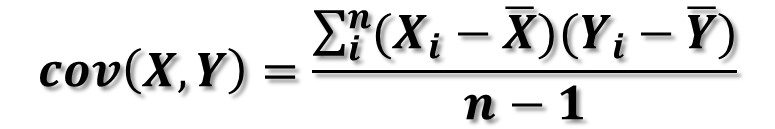
공분산이 양수인 경우, 두 변수는 양의 상관관계를 갖고 있습니다. 이는 한 변수가 증가할 때 다른 변수도 증가한다는 것을 의미합니다. 반면, 공분산이 음수인 경우, 두 변수는 음의 상관관계를 갖고 있습니다. 한 변수가 증가할 때 다른 변수는 감소합니다.
2.1. 해석 시 주의할 점
1. 두 변수가 아무 관계없는 독립 변수 일 경우 = 공분산이 "0"이다.
2. 공분산이 "0"이라고 해서 두 변수가 독립이 아닐 수 있음.

3. 공분산 예시
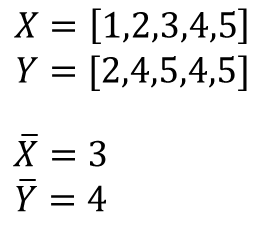
위와 같은 두 변수 X, Y가 다음과 같은 데이터를 갖고 있다고 가정해 보겠습니다. 이를 공분산 식에 대입해 보면 다음과 같습니다. X변수의 평균은 3, Y변수의 평균은 4입니다. 결괏값이 양수이므로 양의 상관관계를 가지고 있습니다.
분모를 n-1로 나누는 이유는 통계학에서의 자유도 보정과 관련이 있습니다. 현재 예시에서는 큰 의미가 없으므로 기존 데이터 개수인 n개로 통칭했습니다.
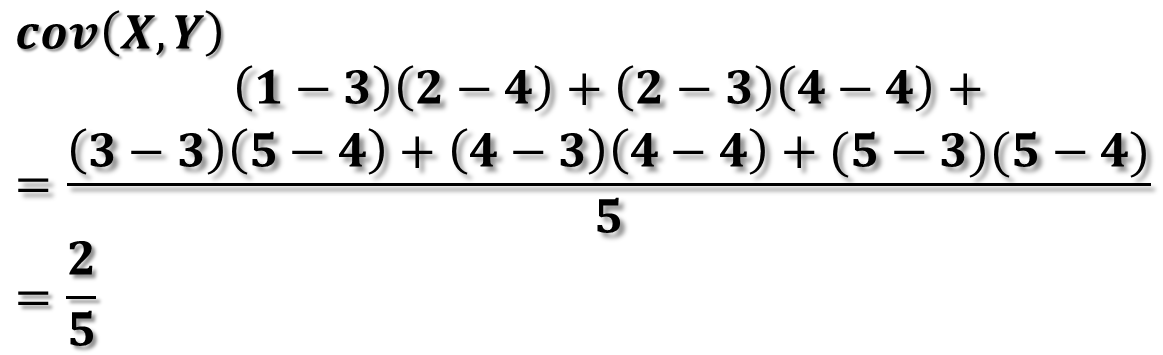
4. 피어슨 상관관계
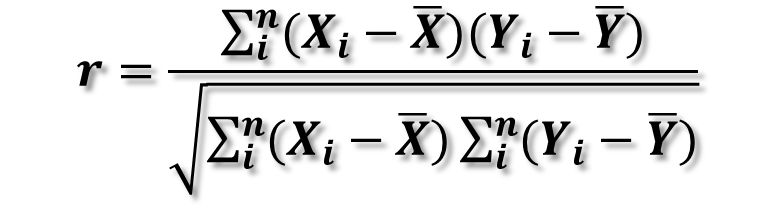
피어슨 상관계수(Pearson Correlation Coefficient)는 두 변수 간의 선형 상관관계를 측정하는 통계적 지표입니다. 이는 두 변수 간의 관계가 얼마나 강하게 선형적으로 연관되어 있는지를 나타냅니다. 피어슨 상관계수는 -1과 1 사이의 값을 가지며, 다음과 같은 공식으로 계산됩니다.
4.1. 공분산과 피어슨상관관계 분석의 차이점
1. 정규화 (Normalization)
- 공분산 단위에 의존적인 단점이 있어서, 데이터의 스케일에 영향을 받습니다.
- 피어슨 상관계수 공분산을 각 변수의 표준편차로 나누어 정규화하여 단위에 덜 민감하게 만듭니다.
2. 범위
- 공분산 -∞에서 +∞까지의 범위를 가집니다.
- 피어슨 상관계수 -1에서 1까지의 범위를 가집니다.
3. 해석 가능성
- 공분산 단위가 제각각인 경우에는 해석이 어려울 수 있습니다.
- 피어슨 상관계수 정규화된 값으로 해석이 용이하며, 1 또는 -1에 가까울수록 강한 상관관계가 있음을 나타냅니다. 0은 상관관계가 없음을 나타냅니다.
4. 상관 정도의 강도
- 피어슨 상관계수 1 또는 -1에 가까우면 강한 선형 상관관계가 있음을 나타냅니다. 0에 가까우면 선형 상관관계가 거의 없다고 판단됩니다.
- 공분산 단위에 따라서 상관 정도를 정확히 해석하기 어렵습니다.
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [통계공부] 13. 이항분포란? 이항분포의 공식과 정규분포와의 관계 (0) | 2024.01.24 |
|---|---|
| [통계공부] 12. 엑셀수식으로 알아보는 정규분포 및 t-분포 (0) | 2024.01.23 |
| [통계공부] 10. 왜도 및 첨도에 대해 알아보기(왜도, 첨도 공식) (0) | 2024.01.21 |
| [통계공부] 9. 평균의 종류(산술평균, 기하평균, 조화평균, 가중평균) (0) | 2023.11.17 |
| [통계공부] 8. 기초통계량의 종류(중심경향성, 퍼짐정도, 왜도, 첨도) (0) | 2023.11.14 |




