1. 왜도 (Skewness)
2023.11.14 - [통계공부] - [통계공부] 8. 기초통계량의 종류(중심경향성, 퍼짐 정도, 왜도, 첨도)
[통계공부] 8. 기초통계량의 종류(중심경향성, 퍼짐정도, 왜도, 첨도)
1. 중심경향성 (Measures of Central Tendency) 중심경향성은 데이터의 중심이 어디에 있는지를 나타내는 통계량을 말합니다. 대표적인 중심경향성 지표로는 평균, 중앙값, 최빈값이 있습니다. 1.1. 평균 (
informyun.com
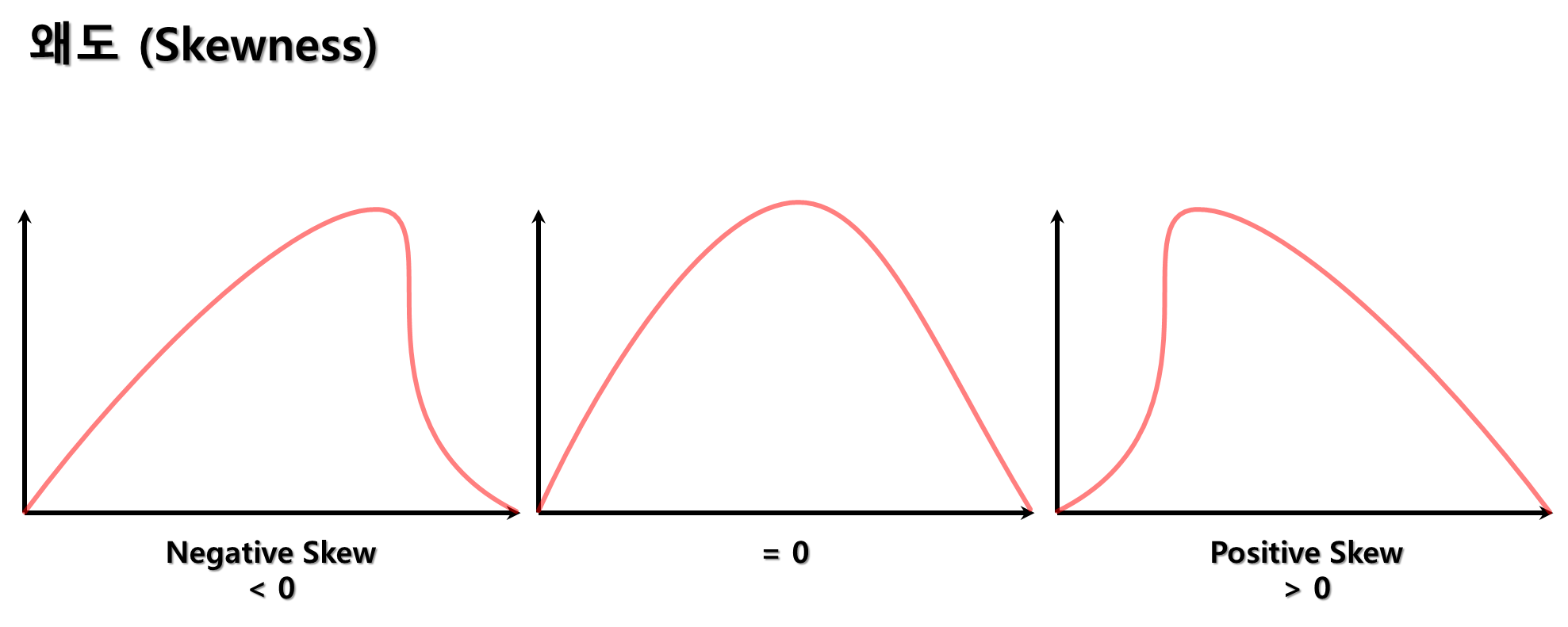
- 왜도는 확률 분포의 비대칭 정도를 나타냅니다.
- 왜도의 부호에 따라 데이터의 비대칭 방향이 결정됩니다.
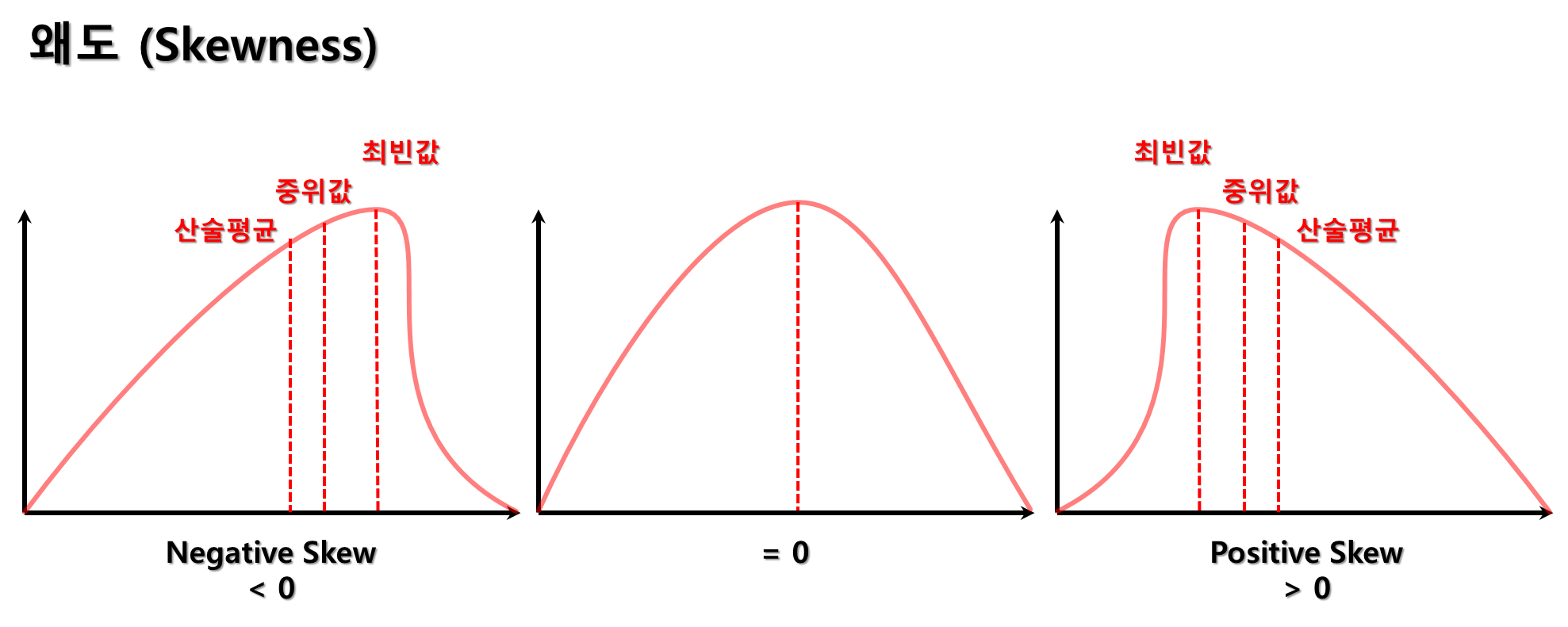
- 왜도가 음수인 경우: 분포가 왼쪽으로 길게 늘어진 꼬리를 가지고 있어 오른쪽으로 치우쳤다고 합니다.
이때, 산술평균→중위값 → 최빈값 순서대로 오른쪽부터 큰 값을 가지고 있습니다.
- 왜도가 양수인 경우: 분포가 오른쪽으로 길게 늘어진 꼬리를 가지고 있어 왼쪽으로 치우쳤다고 합니다.
이때, 최빈값 → 중위값 → 산술평균 순서대로 왼쪽부터 큰 값을 가지고 있습니다.
- 왜도가 0이면 데이터는 대칭 분포를 가지며, 절댓값이 클수록 비대칭 정도가 큽니다.
- 왜도의 절대값이 3 이내의 있으면 정규분포와 비슷하다고 할 수 있습니다.(3이 절대적인 값은 아닙니다.)
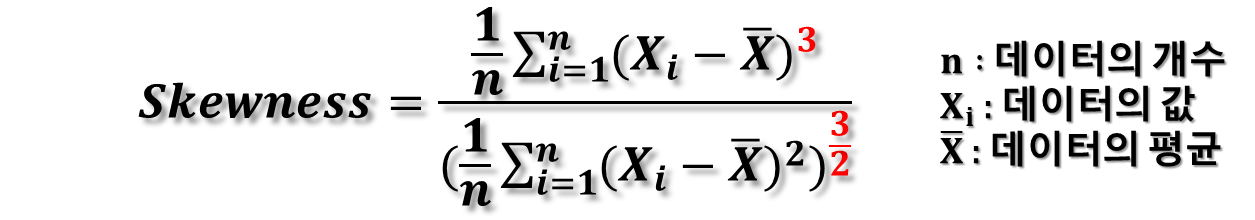
2. 첨도 (Kurtosis)
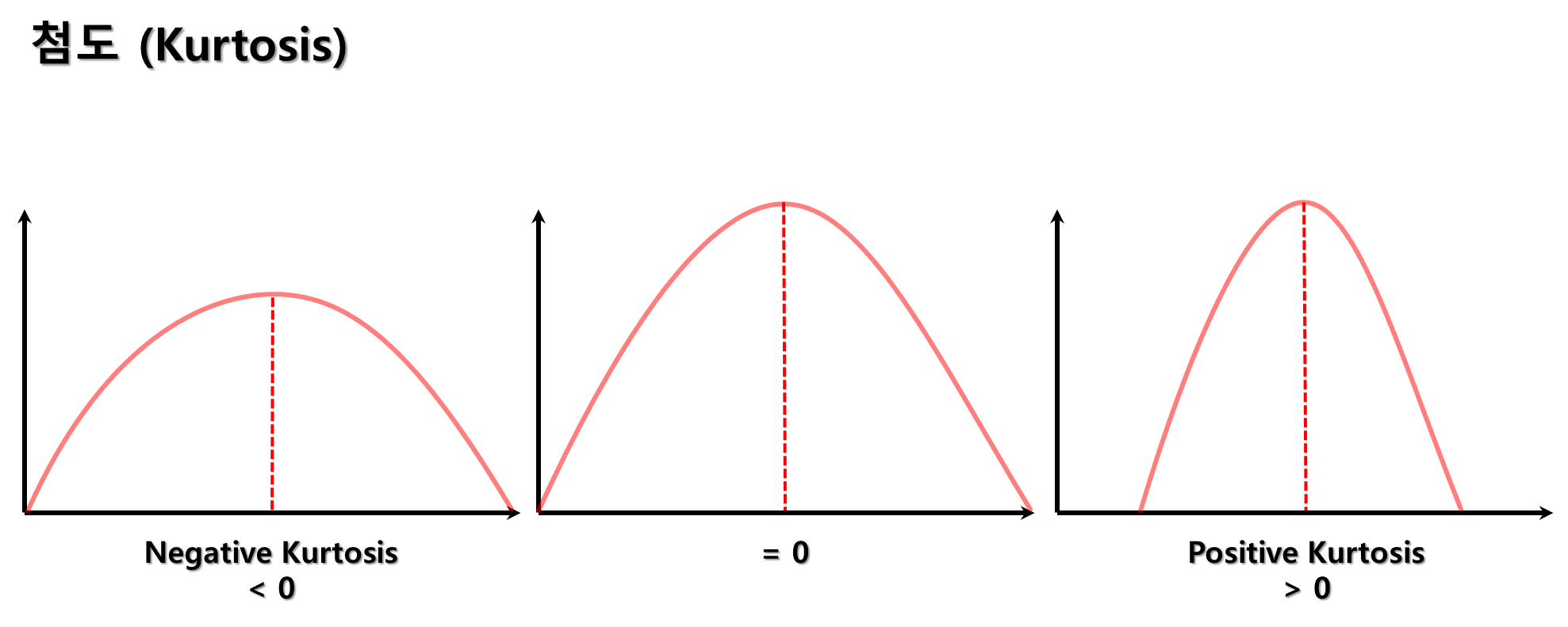
- 첨도는 데이터 분포의 꼬리의 두께를 측정합니다.
- 평균을 중심으로 얼마나 가까이 몰려있는지 나타내는 지표
- 편차가 큰 데이터가 많을수록 커짐(이상치에 영향을 많이 받음)
- 첨도는 정규 분포와 비교하여 얻는데, 정규 분포의 첨도는 0입니다.
- 첨도가 8보다 크면, 분포는 뾰족한 꼬리를 가지고 있어 "길다"라고 표현됩니다. 이를 양수 첨도(positive kurtosis)라고 합니다. (왜도와 마찬가지로 "8"은 절대적인 값이 아닙니다.)
- 첨도가 8보다 작으면, 분포는 뾰족하지 않은 꼬리를 가지고 있어 "짧다"라고 표현됩니다. 이를 음수 첨도(negative kurtosis)라고 합니다. (왜도와 마찬가지로 "8"은 절대적인 값이 아닙니다.)
- 첨도가 0에 가까우면, 분포는 정규 분포와 비슷한 형태를 가지고 있습니다.
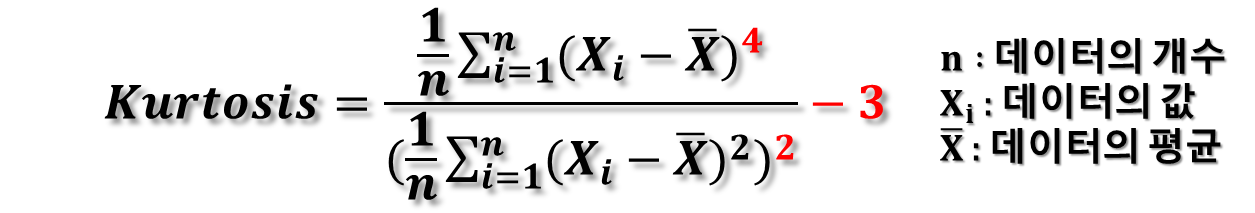
첨도(Kurtosis) 공식에서 왜 마지막에 3을 빼는지에 대한 이유는 정규 분포와의 비교를 간단하게 만들기 위해서입니다. 정규 분포의 첨도는 3이기 때문에, 이 값을 기준으로 하여 비교하는 것이 편리하기 때문입니다.
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [통계공부] 12. 엑셀수식으로 알아보는 정규분포 및 t-분포 (0) | 2024.01.23 |
|---|---|
| [통계공부] 11.공분산 및 피어슨 상관계수 기본 개념 (공분산 공식) (0) | 2024.01.22 |
| [통계공부] 9. 평균의 종류(산술평균, 기하평균, 조화평균, 가중평균) (0) | 2023.11.17 |
| [통계공부] 8. 기초통계량의 종류(중심경향성, 퍼짐정도, 왜도, 첨도) (0) | 2023.11.14 |
| [통계공부] 7. 기술통계와 추론통계의 이해와 차이점 (0) | 2023.11.13 |




