1. 중심경향성 (Measures of Central Tendency)
중심경향성은 데이터의 중심이 어디에 있는지를 나타내는 통계량을 말합니다. 대표적인 중심경향성 지표로는 평균, 중앙값, 최빈값이 있습니다.
1.1. 평균 (Mean)
데이터의 모든 값을 더한 후 데이터의 개수로 나눈 값으로, 데이터의 대략적인 중심을 나타냅니다. 예를 들어, 세 명의 학생의 시험 점수가 각각 70, 80, 90이라면, 평균은 (70 + 80 + 90) / 3 = 80이 됩니다.
또한, 평균의 종류는 다양하면 그중 대표적으로 산술평균, 가중평균, 기하평균등이 있습니다. 이에 관한 내용은 다음 포스팅에서 다루어 보겠습니다.
2023.11.17 - [통계공부] - [통계공부] 9. 평균의 종류(산술평균, 기하평균, 조화평균, 가중평균)
[통계공부] 9. 평균의 종류(산술평균, 기하평균, 조화평균, 가중평균)
1. 산술평균 산술평균은 데이터 집합의 합을 데이터의 개수로 나눈 것입니다. 이는 데이터의 중심 위치를 나타내는 가장 일반적인 지표 중 하나입니다. 산술평균은 이상치에 민감할 수 있어, 데
informyun.com
1.2. 중앙값 (Median)
데이터를 크기 순서로 정렬했을 때 중간에 위치한 값으로, 극단적인 값에 영향을 받지 않는 중심 경향성 지표입니다. 예를 들어, 세 명의 학생의 시험 점수가 70, 80, 90이라면, 중앙값은 80입니다.
1.3. 최빈값 (Mode)
데이터에서 가장 자주 나타나는 값으로, 이산형 데이터의 중심 경향성을 나타냅니다. 만약 세 명의 학생의 시험 점수가 70, 80, 80이라면, 최빈값은 80입니다.
2. 퍼짐 정도 (분산정도, Measures of Dispersion)
퍼짐 정도는 데이터가 얼마나 퍼져있는지를 나타내는 통계량입니다. 주요 퍼짐 정도 지표로는 범위, 분산, 표준편차가 있습니다.
2.1. 범위 (Range)
데이터의 최댓값과 최솟값의 차이를 나타내며, 데이터의 전체적인 퍼짐을 나타냅니다. 예를 들어, 세 명의 학생의 시험 점수가 70, 80, 90이라면, 범위는 90 - 70 = 20입니다.
2.2. 분산 (Variance)
각 데이터가 평균에서 얼마나 떨어져 있는지를 나타내는 지표로, 제곱된 편차의 평균입니다. 예를 들어, 세 명의 학생의 시험 점수가 70, 80, 90이라면, 분산을 계산할 때 (70-80)^2, (80-80)^2, (90-80)^2를 각각 구하여 더하고 변량의 수로 나누어 존 값입니다.
2023.10.23 - [전체글] - [통계공부] 2.평균, 편차, 분산, 표준편차
[통계공부] 2.평균, 편차, 분산, 표준편차
1. 평균 (Mean) 평균은 데이터 집합의 중심 위치를 나타내는 통계적 지표로, 모든 데이터 포인트의 합을 데이터의 개수로 나눈 값입니다. 이것은 데이터의 대표값 중 하나로, 집단의 전반적인 경향
informyun.com
2.3. 표준편차 (Standard Deviation)
분산의 제곱근으로, 데이터의 퍼짐 정도를 측정하는 데 사용됩니다. 표준편차는 분산의 제곱근으로 계산됩니다.
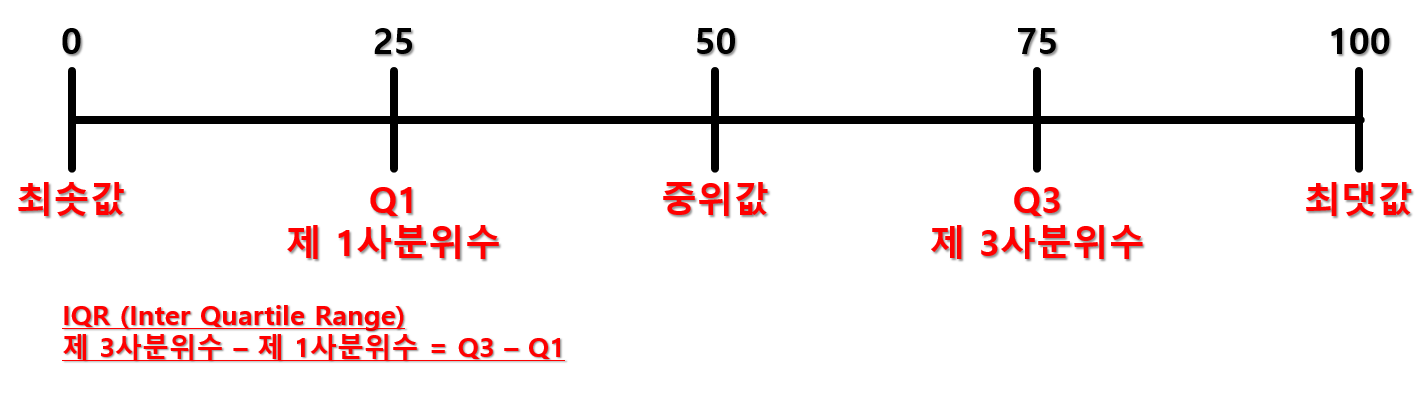
2.4. IQR (Interquartile Range)
데이터의 중간 50% 범위를 나타내는 지표로, 데이터의 상위 75%와 하위 25%의 중간 범위입니다. 이는 데이터의 극단값에 민감하지 않고 중간 범위를 나타내므로 이상치에 영향을 받지 않습니다. IQR은 데이터를 정렬하고 상위 25%에 해당하는 3/4 지점과 하위 25%에 해당하는 1/4 지점의 차이입니다.
3. 왜도와 첨도 (Skewness and Kurtosis)
왜도와 첨도는 데이터 분포의 비대칭성과 뾰족한 정도를 나타내는 통계량입니다. 왜도와 첨도는 다음 포스팅에서 더 자세히 다루어 보겠습니다.
3.1. 왜도 (Skewness)
데이터 분포가 얼마나 비대칭인지를 나타내는 지표로, 왜도가 0이면 대칭이며, 양수일 경우 오른쪽으로, 음수일 경우 왼쪽으로 비대칭합니다. 예를 들어, 왜도가 양수인 경우, 평균은 중앙값보다 오른쪽에 위치합니다.
3.2. 첨도 (Kurtosis)
데이터 분포의 꼬리의 두께 또는 뾰족한 정도를 나타내는 지표로, 첨도가 3에 가까우면 정규 분포에 가깝고, 3보다 크면 뾰족하며, 3보다 작으면 둥글다고 판단합니다.
2024.01.21 - [전체글] - [통계공부] 10. 왜도 및 첨도에 대해 알아보기(왜도, 첨도 공식)
[통계공부] 10. 왜도 및 첨도에 대해 알아보기(왜도, 첨도 공식)
1. 왜도 (Skewness) 2023.11.14 - [통계공부] - [통계공부] 8. 기초통계량의 종류(중심경향성, 퍼짐 정도, 왜도, 첨도) [통계공부] 8. 기초통계량의 종류(중심경향성, 퍼짐정도, 왜도, 첨도) 1. 중심경향성 (Me
informyun.com
4. 예시
예시 데이터는 포스팅 하단에 있는 엑셀 파일을 참고해주세요.
학생 100명의 키를 전체 데이터로 놓고 분석하겠습니다. 히스토그램으로 그려보니 어느 정도 정규분포의 모양을 가져 보입니다. 엑셀에 있는 함수를 통해 각각의 기초통계량을 구해봤습니다.
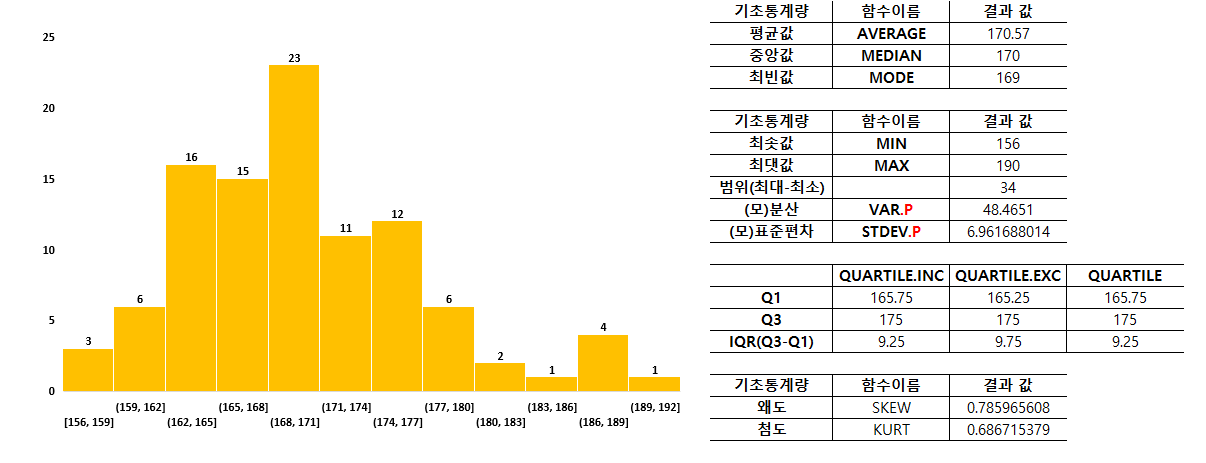
기본적으로 100명의 학생 평균 키는 170.57cm이며 중앙값은 170cm, 가장 자주 등장한 최빈값은 169cm입니다.
가장 작은 키를 가진 학생은 156cm이며, 가장 큰 키는 190cm로, 해당 데이터의 범위는 둘의 차인 34입니다.
사분위수인 IQR을 구해 보겠습니다. 상위 75%인 Q3와 하위 25%인 Q1의 차로 구할 수 있습니다.
엑셀 함수에서 =QUARTILE을 치면, 3종류가 나오게 됩니다. 아래내용을 참고해 주세요.

왜도는 0.79 정도로 일단, 양수이기 때문에 평균이 중앙값보다 오른쪽에 위치한다는 것을 알 수 있습니다. (평균이 오른쪽으로 살짝 치우쳐졌다.)
첨도는 0.69로 3보다 작기 때문에 둥근 모습(뾰족하지 않다.)을 하고 있다는 것을 알수 있습니다.
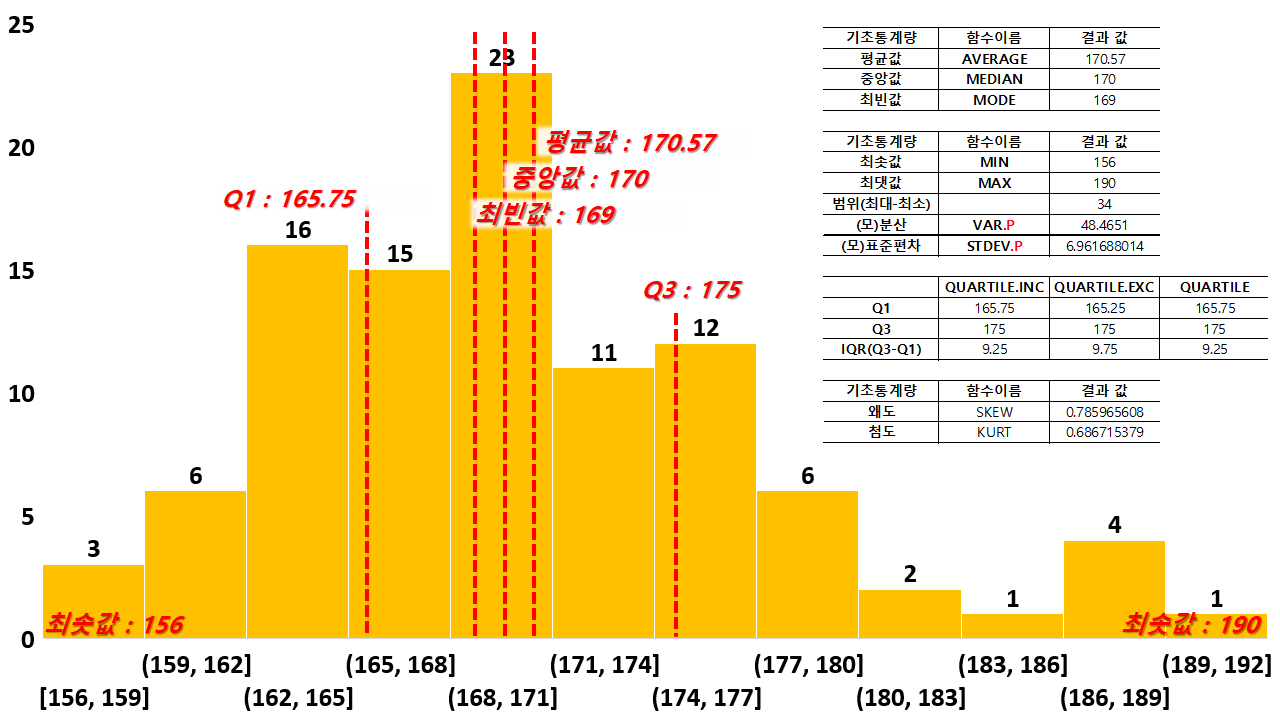
이는, 엑셀 기본 기능인 데이터 분석 기능의 기술통계법을 사용해서 결과를 도출해도 같습니다. 해당 내용도 추후에 다루어 보겠습니다.
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [통계공부] 10. 왜도 및 첨도에 대해 알아보기(왜도, 첨도 공식) (0) | 2024.01.21 |
|---|---|
| [통계공부] 9. 평균의 종류(산술평균, 기하평균, 조화평균, 가중평균) (0) | 2023.11.17 |
| [통계공부] 7. 기술통계와 추론통계의 이해와 차이점 (0) | 2023.11.13 |
| [통계공부] 6. 모집단, 표본집단 그래프로 이해하기(예시문제) (0) | 2023.10.30 |
| [통계공부] 5. 모집단과 표본집단 (신뢰구간 및 신뢰도 공식) (0) | 2023.10.28 |




