1. 평균 (Mean)
평균은 데이터 집합의 중심 위치를 나타내는 통계적 지표로, 모든 데이터 포인트의 합을 데이터의 개수로 나눈 값입니다. 이것은 데이터의 대표값 중 하나로, 집단의 전반적인 경향을 파악하는 데 사용됩니다.
평균 = (모든 데이터 값의 합) / (데이터 개수)
평균은 중심 경향을 파악할 때 유용하며, 예를 들어, 평균 급여, 평균 시간, 평균 성적 등을 계산하는 데 자주 사용됩니다.

2. 편차 (Deviation)
편차는 각 데이터 포인트와 평균 간의 차이를 나타내는 값입니다. 편차는 데이터가 어떻게 평균 주변에 분포하는지를 이해하는 데 도움을 줍니다.
편차 = 각 데이터 값 - 평균
편차는 각 데이터 값이 평균으로부터 얼마나 떨어져 있는지를 측정합니다. 이것은 데이터 분석에서 개별 데이터 포인트의 상대적 위치를 이해하는 데 도움을 줍니다.
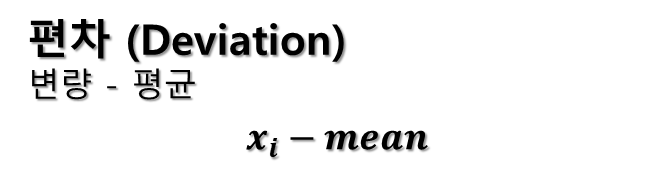
3. 분산 (Variance)
분산은 데이터 포인트의 편차를 제곱한 값들의 평균으로, 데이터의 변동성을 나타내는 중요한 지표입니다. 분산이 클수록 데이터가 평균 주변에 흩어져 분포되어 있음을 의미합니다.
1. 각 데이터 값에서 평균을 뺀 후, 그 결과를 제곱합니다.
2. 이러한 제곱된 편차들을 모두 더한 후, 데이터의 개수로 나눕니다.
분산은 데이터의 분포와 데이터 포인트가 어떻게 평균 주변에 퍼져 있는지를 측정하는 데 사용됩니다.

4. 표준편차 (Standard Deviation)
표준편차는 분산의 양의 제곱근으로, 데이터의 변동성을 나타내는 중요한 지표입니다. 표준편차는 데이터 포인트가 평균에서 어느 정도 떨어져 있는지를 측정하는 데 사용됩니다.
표준편차 = 분산의 제곱근 = √(분산)
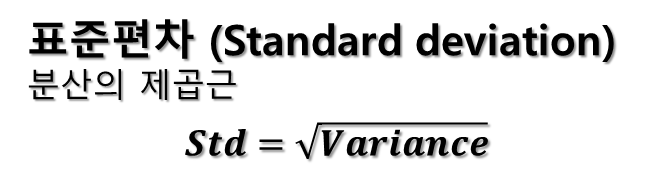
표준편차는 분산과 동일한 단위를 갖고 있으며, 분포의 형태와 데이터의 흩어진 정도를 파악하는 데 도움을 줍니다. 작은 표준편차는 데이터가 평균 주변에 밀집되어 있는 것을 나타내고, 큰 표준편차는 데이터가 더 넓게 분포되어 있음을 나타냅니다.
5. 예시
[통계공부] 1. 변량,도수,도수분포표,상대도수,히스토그램
1. 변량 (Variable): 변량은 연구나 관찰 대상에서 관심을 가지는 속성 또는 특성을 나타냅니다. 예를 들어, 학생들의 키, 나이, 성적 등은 모두 변량입니다. 이러한 변량은 데이터 분석의 기반을 형
informyun.com
위 포스팅에서 사용한 성적관련 변량을 이용해 표준편차까지 구하고, 비교해보겠습니다. 예시 파일은 아래에서 다운해주세요.
기존 A학급과 A 학급과 비교하기 위한 B학급을 새로 만들었습니다. 두 학급 모두 각각 100명의 학생이 있습니다.
확인 결과 A 학급의 평균은 67.39이며, B 학급의 평균은 67.66 으로 거의 같다가 봐도 무방합니다. 이제, 표준편차도 확인해보겠습니다. A학급의 표준편차는18.09이며, B 학급의 표준편차는 15.93입니다.
표준편차의 의미는 평균으로 부터 변량(데이터, 학생의 점수)의 분포가 퍼져있는지를 나타냅니다.
분산이 크다 = 표준편차가 크다.
표준편차가 크다 = 변량(값)들이 평균으로 부터 넓게 퍼져있다.
표준편차가 작다 = 변량(값)들이 평균을 중심으로 집중해 있다.
즉, 두 학급의 평균은 같지만 B학급의 표준편차가 더 작기 때문에 평균을 중심으로 A 학급보다 더 많이 집중되어 있다는 것을 수치를 통해 확인 할 수 있습니다. 해당 수치를 그래프로 나타내면 아래와 같습니다.
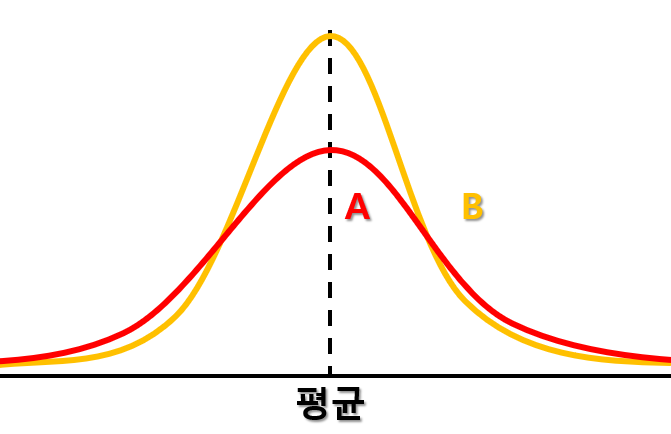
그래프에서 확인 할 수 있듯이 B 학급이 평균을 중심으로 더 모여 있으며 가파른 모습을 보이고, A 학급은 B 학급 대비 완만한 그래프 형태를 보여줍니다.
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [통계공부] 6. 모집단, 표본집단 그래프로 이해하기(예시문제) (0) | 2023.10.30 |
|---|---|
| [통계공부] 5. 모집단과 표본집단 (신뢰구간 및 신뢰도 공식) (0) | 2023.10.28 |
| [통계공부] 4. 표준정규분포 및 표준화 (예시문제 학습) (0) | 2023.10.25 |
| [통계공부] 3. 정규분포의 특징과 수식 (0) | 2023.10.24 |
| [통계공부] 1. 변량,도수,도수분포표,상대도수,히스토그램 (0) | 2023.10.22 |




