1. 모집단과 표본집단
1.1. 모집단 (Population)
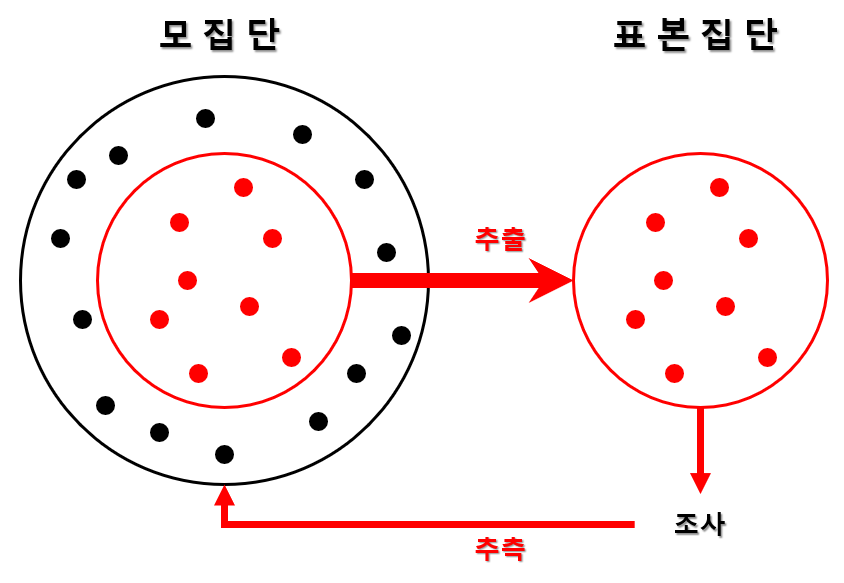
- 모집단은 특정 관심 대상의 전체 집합을 나타냅니다. 이것은 연구자가 조사하려는 모든 개체 또는 항목을 포함합니다. 모집단은 종종 크고 다양하며, 관심 대상에 따라 다를 수 있습니다.
- 예를 들어, 만약 특정 제품의 품질을 조사하고자 한다면 해당 제품의 모든 제품이 모집단이 될 것이며, 모든 사람의 연령을 조사하려면 모든 인구가 모집단이 될 것입니다.
1.2. 표본집단 (Sample)
- 표본집단은 모집단에서 무작위로 선택된 부분 집합을 나타냅니다. 표본은 모집단을 대표하고자 하는 목적으로 사용됩니다.
- 표본집단은 모집단에서 데이터 수집의 비용, 시간 및 노력을 줄이는 데 도움을 줍니다. 또한 통계적 분석 및 추론을 수행할 때 표본 데이터를 사용하여 모집단에 대한 정보를 얻을 수 있습니다.
1.3. 표본평균, 표본분산, 표본표준편차
<표본평균>
표본평균은 주어진 표본 데이터의 값들의 합을 표본 크기로 나눈 것입니다. 표본 데이터의 중심 경향을 나타내는 지표로 사용됩니다.
<표본분산>
표본분산은 표본 데이터의 분포에서 데이터 포인트들이 평균으로부터 얼마나 퍼져 있는지를 나타내는 지표입니다. 높은 분산은 데이터가 평균 주변에 퍼져 있음을 나타냅니다.
<표본표준편차>
표본표준편차는 표본분산의 제곱근으로, 분산의 단위를 원래 데이터의 단위로 돌려주는 역할을 합니다. 데이터 분포의 변동성을 더 직관적으로 이해할 수 있게 도와줍니다.

표본분산에서 편차의 제곱의 합을 n-1로 나누는 이유
표본분산의 분모를 n-1로 나누는 이유는 통계학에서의 자유도 보정과 관련이 있습니다. 이러한 보정은 표본분산이 모집단 분산을 더 정확하게 추정하기 위한 것이며, 표본 통계량의 특성을 보다 잘 나타낼 수 있게 도와줍니다.
이는 수식으로도 설명이 가능합니다. 아래 타 블로그에서 자세히 다루고 있습니다.
https://ladyang86.tistory.com/183
그러나, 표본의 크기가 일정 이상 커지게 되면 n으로 나누나, n-1로 나누나 결과값에 큰 변화는 없습니다.
2. 신뢰구간과 신뢰도
2.1. 신뢰구간 (Confidence Interval)
- 신뢰구간은 특정 확률로 모수(예를 들면 평균)의 추정값이 포함될 가능성을 나타내는 구간이며, 신뢰도는 이 구간이 모수를 얼마나 정확하게 추정하는지를 나타냅니다.
- 보통 신뢰구간은 표본 데이터로부터 계산되며, 평균, 분산, 표준편차 등의 모수 추정에 사용됩니다.
2.2. 신뢰도 (Confidence Level)
- 신뢰도는 신뢰구간에 대한 신뢰 정도를 나타내는 확률입니다. 일반적으로 90%, 95%, 99% 등과 같은 백분율로 표시됩니다.
- 더 높은 신뢰도를 가지려면 신뢰구간의 폭이 더 넓어집니다. 이것은 모수 추정의 정확도를 나타냅니다.
3. 신뢰구간 공식 유도
3.1. 신뢰도 선정
신뢰구간을 선정할때는 먼저 신뢰도를 선정해줍니다. 신뢰도는 보통 90%, 95%, 99% 로 설정합니다. (신뢰도 100%는 전체 범위이므로 선정하는 의미가 없음)
이 포스팅에서는 95%를 예시로 계산해 보겠습니다.
신뢰도를 95%로 선정한다는 말은 임의로 선정한 표본을 표준정규분포곡선의 맞게 "표준화" 하였을때 면적 0.95안에 들어갈 확률이다. 라고 말을 바꿔 설명할 수 있습니다.
그렇다면, 먼저 표준정규분포곡선에서 평균"0"을 기준으로 넓이(=면적) 이 0.95가 되는 x 좌표를 찾아 보겠습니다.
지난 시간에 공부한 표준정규분포 공식을 구간적분해 보겠습니다.
2023.10.24 - [전체글] - [통계공부] 3. 정규분포의 특징과 수식
[통계공부] 3. 정규분포의 특징과 수식
1. 정규분포: 확률 분포의 핵심 정규분포는 확률과 통계학에서 핵심적인 역할을 하는 확률 분포 중 하나입니다. 이 분포는 다양한 현상과 데이터 세트에서 관찰되며, 평균과 표준편차를 통해 완
informyun.com
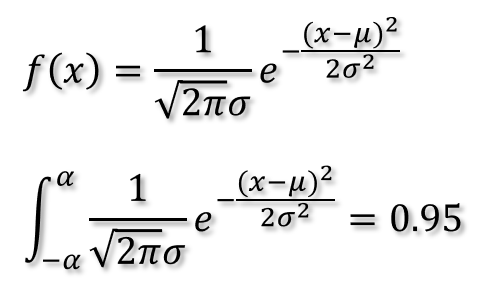
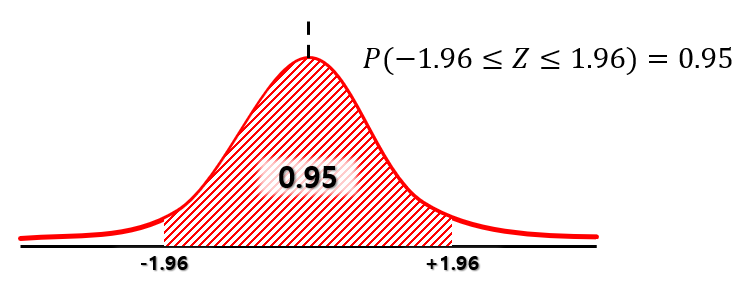
표준정규분포 곡선을 -α 부터 α까지 범위에 대해 적분 했을때 0.95가 나오는 α의 값은"1.96" 입니다.
즉, 표준정규분포 곡선을 -1.96부터 1.96까지 적분했을때 면적이 0.95입니다.
이제, 임의로 선정한 표본의 평균인 X(bar)에 대해 표준화 해 보겠습니다. 표준화 하여 나타 내면 아래와 같습니다.
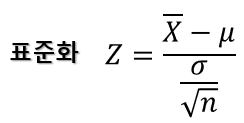
이를 위 공식에 대입하여 모평균에 대해 정리하면 아래와 같습니다.
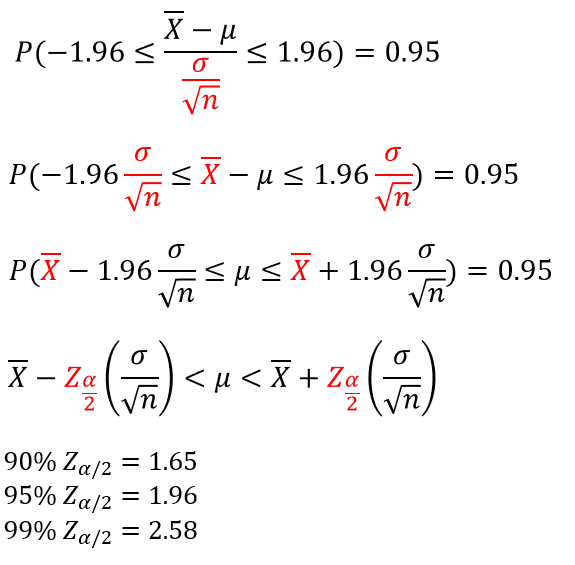
이외에도 신뢰도 90%일때는 1.65 신뢰도 99%일때는 2.58의 값을 가집니다. 해당 내용은 아래 파워포인트 첨부하겠습니다. 다음 포스팅에서는 위에서 설명한 내용을 직접 그래프로 그려보고, 예시문제도 풀어 보겠습니다. 감사합니다.
4. 추가 사항
- 신뢰구간과 신뢰도는 통계학에서 중요한 개념이며, 다양한 분야에서 활발하게 활용됩니다.
- 통계학에서는 다양한 분포를 사용하여 신뢰구간을 계산하며, 정규분포는 가장 흔하게 사용되는 분포 중 하나입니다.
- 표본의 크기가 커질수록 신뢰구간의 폭이 좁아지며, 모수 추정의 정확도가 향상됩니다.
- 신뢰도 수준은 연구자의 의사 결정에 영향을 미치며, 더 높은 신뢰도는 더 넓은 신뢰구간을 생성합니다.
- 통계적 추론은 불확실성을 고려하여 결정을 내릴 때 매우 유용하며, 실험, 조사 및 조사 연구에서 널리 활용됩니다.
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [통계공부] 7. 기술통계와 추론통계의 이해와 차이점 (0) | 2023.11.13 |
|---|---|
| [통계공부] 6. 모집단, 표본집단 그래프로 이해하기(예시문제) (0) | 2023.10.30 |
| [통계공부] 4. 표준정규분포 및 표준화 (예시문제 학습) (0) | 2023.10.25 |
| [통계공부] 3. 정규분포의 특징과 수식 (0) | 2023.10.24 |
| [통계공부] 2.평균, 편차, 분산, 표준편차 (0) | 2023.10.23 |




