1. 정규분포: 확률 분포의 핵심
정규분포는 확률과 통계학에서 핵심적인 역할을 하는 확률 분포 중 하나입니다. 이 분포는 다양한 현상과 데이터 세트에서 관찰되며, 평균과 표준편차를 통해 완전하게 정의됩니다. 아래에서 정규분포의 특징, 수식, 활용, 그리고 중요성에 대해 자세히 알아보겠습니다.
2. 정규분포의 특징
1. 대칭성
정규분포는 평균을 중심으로 좌우 대칭을 이루는 형태를 갖습니다. 이는 데이터가 평균 주변에 대체로 균등하게 분포한다는 것을 의미합니다.
2. 평균과 중앙값 동일
정규분포의 평균값과 중앙값(중위수)은 동일합니다. 이는 분포의 중심이 평균에 위치한다는 것을 나타냅니다.
3. 정점 위치
정규분포의 종 모양 모양은 정규분포의 정점(peak)이 평균에 위치한다는 특징을 가지고 있습니다.
4. 표준편차의 영향
정규분포의 폭은 표준편차에 의해 결정됩니다. 표준편차가 작을수록 분포는 뾰족한 형태를 갖고, 표준편차가 클수록 분포는 보다 완만한 형태를 나타냅니다.
3. 정규분포의 수식
정규분포의 수식은 아래와 같습니다.
지오 지브라 홈페이지에서 해당 그래프를 그려보면 아래와 같습니다. (표준정규분포 : 표준편차=1, 평균=0 인 그래프)
https://www.geogebra.org/?lang=ko
지오지브라 - 1억 명 이상의 학생과 교사가 사용하는 세계에서 가장 인기있는 무료 수학 학습 도
클래스 활동, 그래프, 기하, 공동 화이트보드 등을 위한 무료 디지털 학습 도구
www.geogebra.org


4. 정규분포의 수식 (엑셀을 통한 시각화 : 표준정규분포)
엑셀의 수식및 그래프삽입 기능을 통해 정규분포 변화를 시각화 해봤습니다. 해당 엑셀 파일은 아래에서 다운해주세요.
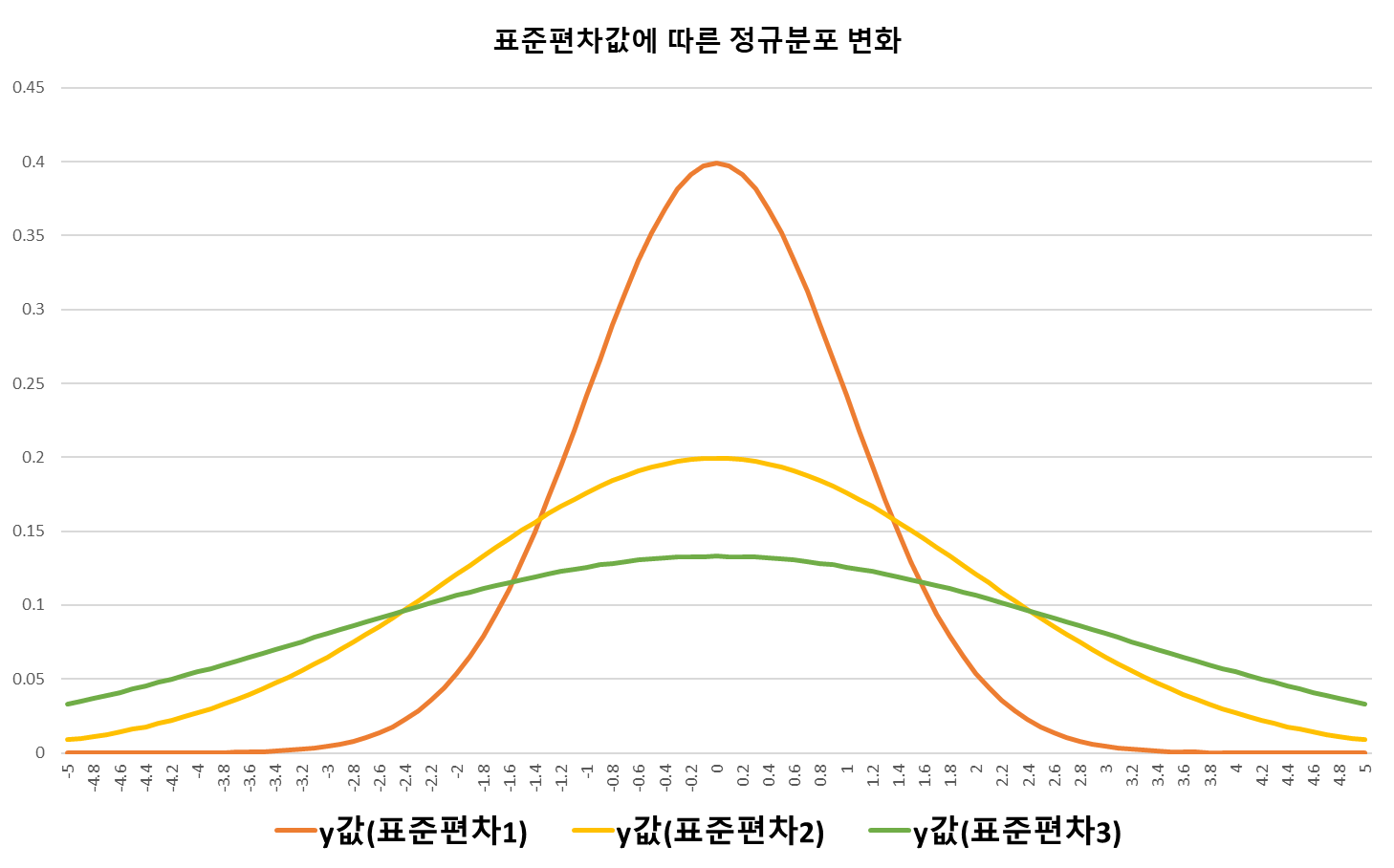
먼저, 첫번째 그래프는 평균은 동일하게 "0"으로 고정한 상태에서 표준편차 값만 "1", "2", "3," 으로 변경 했을 때 그래프 입니다. 전 시간에 학습한 표준편차 값에 따른 평균을 중심으로 변량이 얼마나 밀집되어 있는가(그래프의 완만정도)를 확인 할 수 있습니다.
표준편차가 1인 그래프가 가장 평균을 중심으로 데이터가 밀집되어 있으며, 표준편차가 3인 그래프가 가장 완만한 형태를 보이고 있습니다.
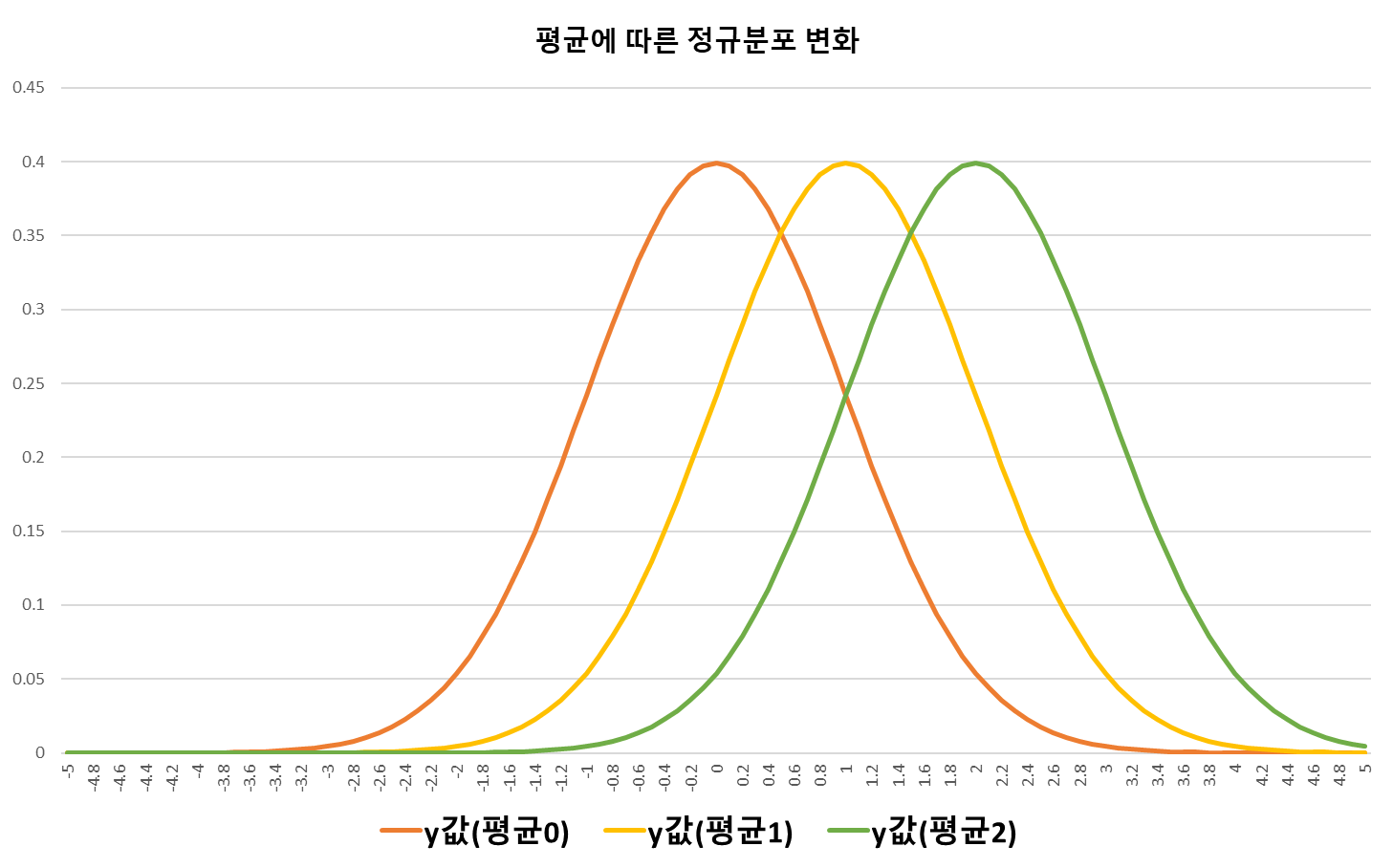
두번째, 그래프는 표준편차값은 고정인 상태에서 평균만 변경했을때의 그래프 모습입니다. 사실 굳이 그리지 않아도, 직감적으로 어떻게 생길지 알것 같으나, 직접 확인을 위해 그려 봤습니다.
예상대로 그래프의 가파름/완만함의 변화는 없고, 평균값(Peak, 봉우리)만 설정한대로 이동하는 모습을 보여줬습니다.
다음시간에는 정규분포를 통한 표준화와 표준화의 중요성에 대해 학습해 보겠습니다.
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [통계공부] 6. 모집단, 표본집단 그래프로 이해하기(예시문제) (0) | 2023.10.30 |
|---|---|
| [통계공부] 5. 모집단과 표본집단 (신뢰구간 및 신뢰도 공식) (0) | 2023.10.28 |
| [통계공부] 4. 표준정규분포 및 표준화 (예시문제 학습) (0) | 2023.10.25 |
| [통계공부] 2.평균, 편차, 분산, 표준편차 (0) | 2023.10.23 |
| [통계공부] 1. 변량,도수,도수분포표,상대도수,히스토그램 (0) | 2023.10.22 |




