1. 표준정규분포(Standard Normal Distribution)
표준정규분포는 평균이 0이고 표준편차가 1인 정규분포를 의미합니다. 이 분포는 종 모양의 곡선으로, 정규분포를 따르는 확률 변수를 표준화하는 데 사용됩니다.
표준정규분포를 따르는 확률 변수는 Z로 표시되며, 평균을 0, 표준편차를 1로 조정한 값이 Z 값입니다. 표준정규분포의 확률 밀도 함수는 다음과 같이 표현됩니다

표준정규분포는 통계 분석에서 중요한 이유는 다음과 같습니다
- 데이터를 표준정규분포로 표준화하면, 서로 다른 데이터 집단을 비교하거나 통계 분석하기가 더 쉬워집니다.
- 통계적 가설 검정에서 p-값을 계산하는 데 사용됩니다.
2. 표준화(Standardization)
표준화는 데이터의 평균을 0으로, 표준편차를 1로 조정하여 데이터를 새로운 척도로 변환하는 프로세스입니다. 표준화는 다음과 같은 방식으로 수행됩니다
1. 각 데이터 포인트에서 평균을 뺍니다.
2. 그 후, 각 데이터를 표준편차로 나눕니다. 이로써 데이터의 스케일이 표준편차의 크기에 맞게 조정됩니다.
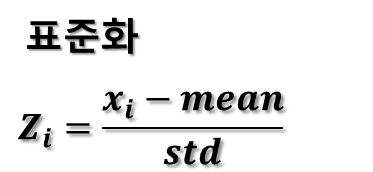
표준화를 통해 데이터의 단위나 척도에 관계없이 데이터를 표준정규분포로 변환할 수 있습니다.
표준화는 주로 다음과 같은 상황에서 사용됩니다
- 다른 데이터 집단 간의 비교를 용이하게 하려고 할 때.
- 회귀 분석 또는 다차원 공간에서 변수 간의 중요성을 비교할 때.
- 이상치를 식별하고 제거할 때.
3. 표준화 예시 문제
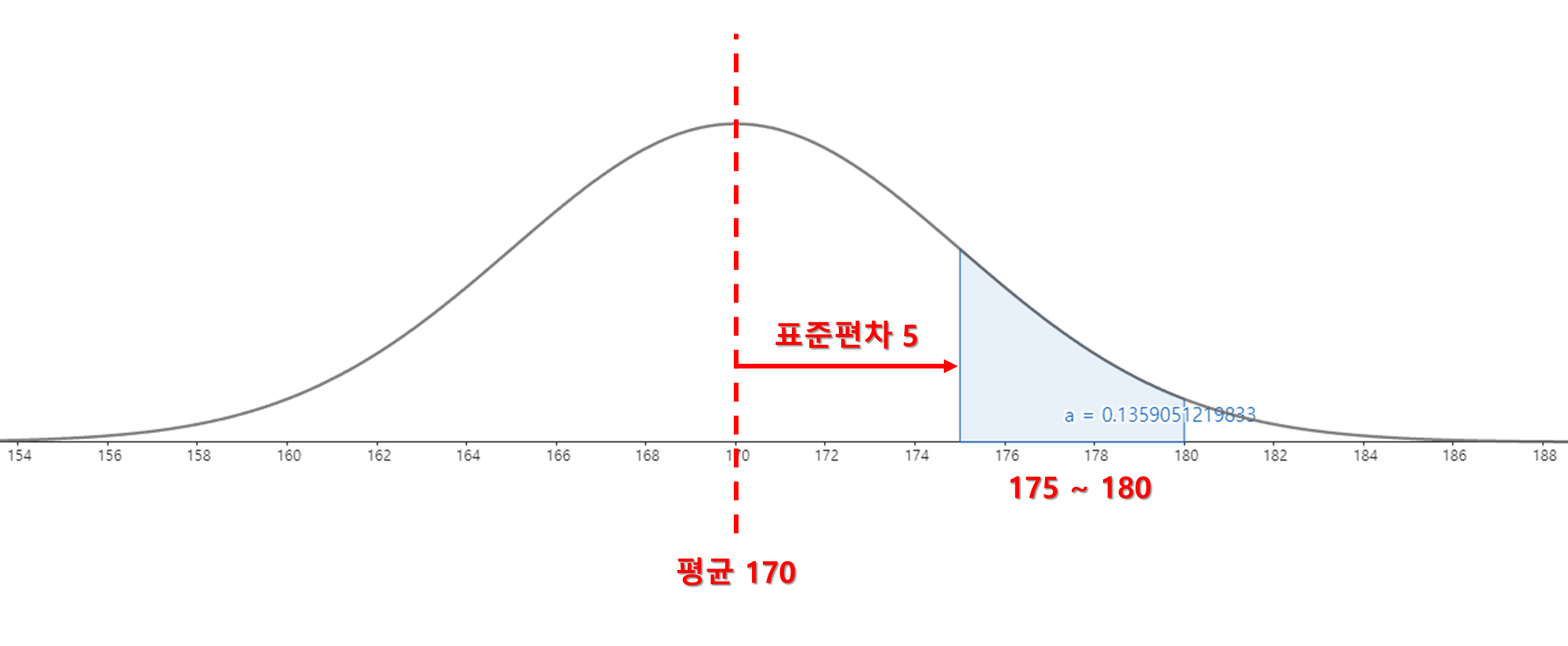
예시) 한국남성의 신장 조사시 평균이 170, 표준편차가 5인 정규분포이다.
한 남자의 키가 175 ~ 180일 확률은?
3.1. 표준화 없이
문제에서 주어진 조건을 통해 확률을 구할 수 있습니다.
해당 조건으로 그래프를 그리면 아래와 같습니다. 답은 0.135로 13.5% 입니다.

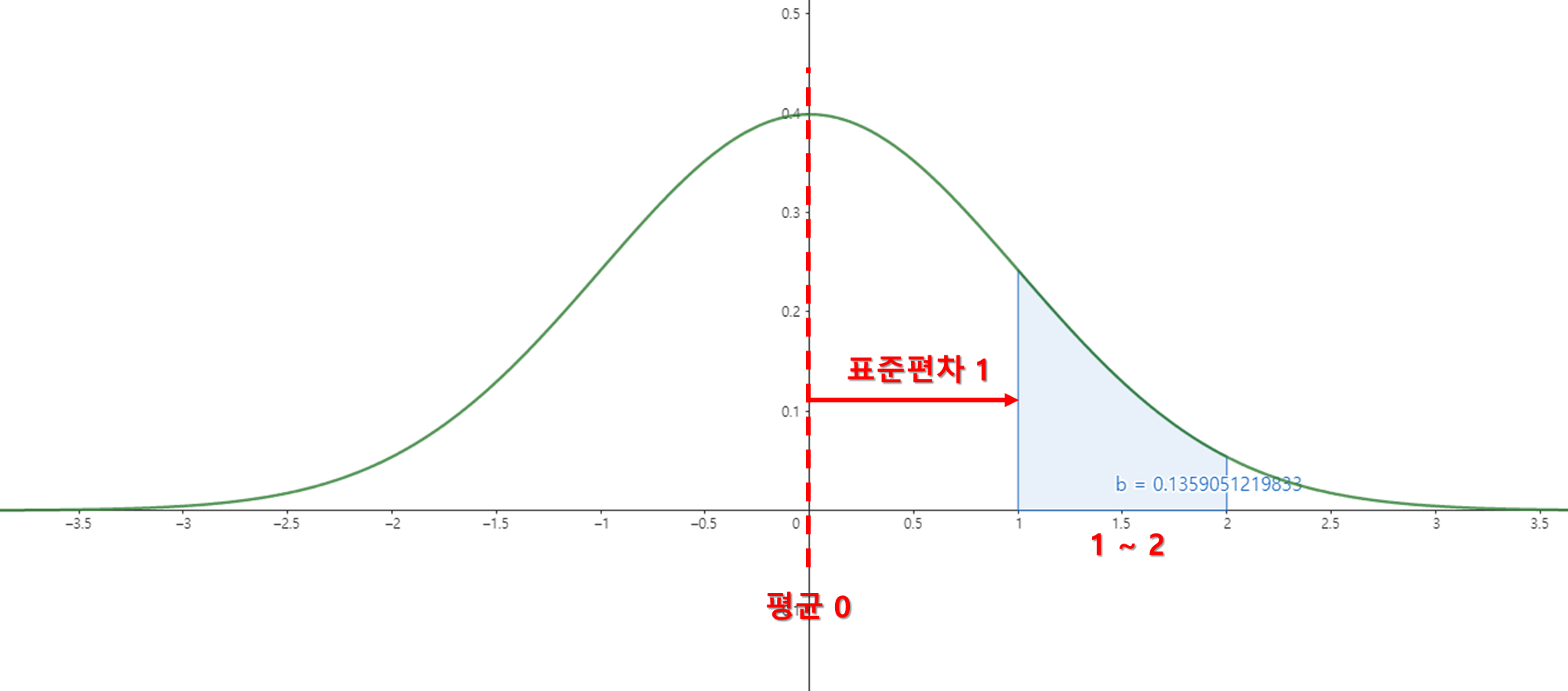
3.1. 표준화를 이용
표준화과정을 통해 해당 정규분포를 표준정규분포 틀에 맞게 변경하여, 답을 구하는 과정입니다.
역시, 정답은 표준화 없이 구한 것과 동일하게 0.135가 나왔습니다. 표준화 과정에서 각 데이터에서 평균을 빼고 표준편차를 나누는 과정에서 그래프의 스케일을 표준정규분포에 맞게 조정했기 때문입니다.
해당 표준화 과정때문에 수식이 더 길어보일수 있으나, 과학실험 및 현상 분석시 다양한 집단을 분석하게 됩니다.
이때 데이터의 단위 및 스케일이 다를때, 직접 비교가 어렵습니다. 때문에, 표준화 과정을 이용하면 이와 같은 문제를 해결 할 수 있습니다.
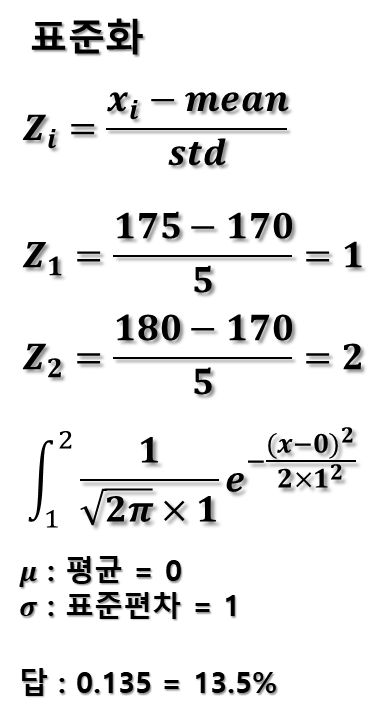
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [통계공부] 6. 모집단, 표본집단 그래프로 이해하기(예시문제) (0) | 2023.10.30 |
|---|---|
| [통계공부] 5. 모집단과 표본집단 (신뢰구간 및 신뢰도 공식) (0) | 2023.10.28 |
| [통계공부] 3. 정규분포의 특징과 수식 (0) | 2023.10.24 |
| [통계공부] 2.평균, 편차, 분산, 표준편차 (0) | 2023.10.23 |
| [통계공부] 1. 변량,도수,도수분포표,상대도수,히스토그램 (0) | 2023.10.22 |




