1. 산술평균
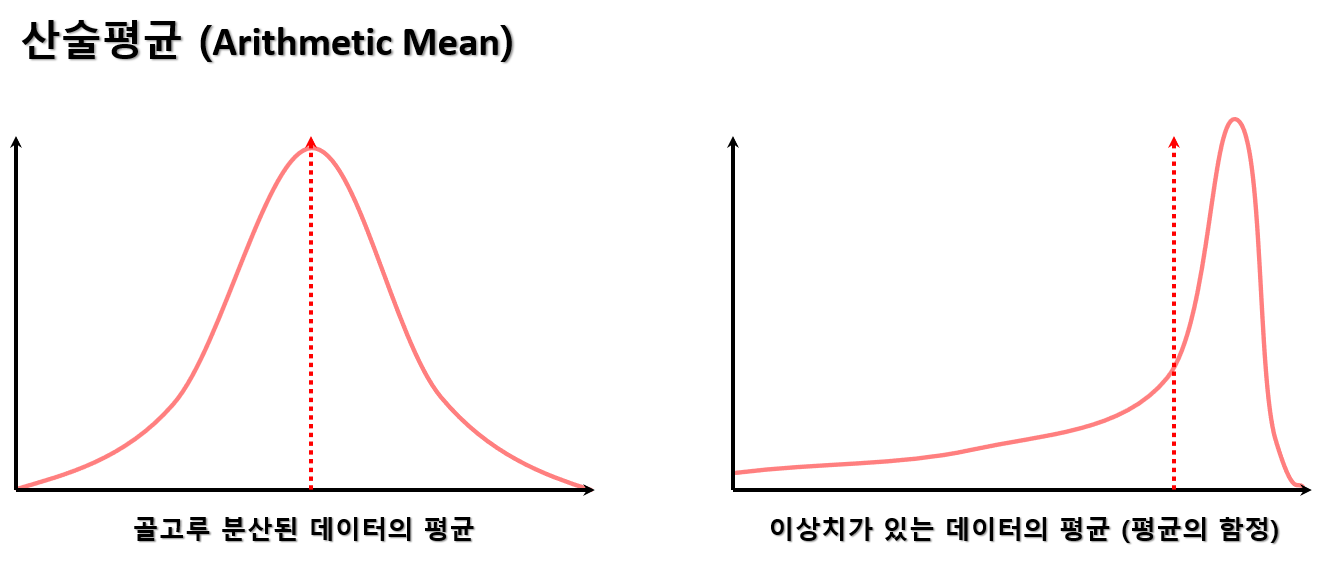
산술평균은 데이터 집합의 합을 데이터의 개수로 나눈 것입니다. 이는 데이터의 중심 위치를 나타내는 가장 일반적인 지표 중 하나입니다. 산술평균은 이상치에 민감할 수 있어, 데이터의 분포가 비대칭이거나 이상치가 있는 경우에는 다른 평균들과 비교하여 조심해야 합니다.
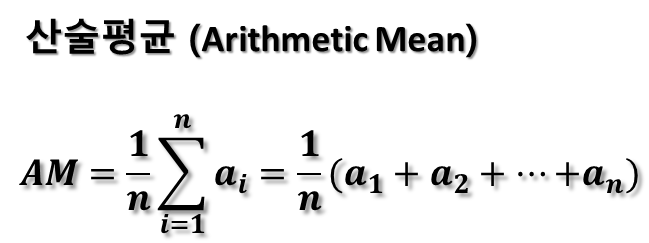
2. 기하평균
기하평균은 양수로 이루어진 데이터 집합의 값들을 모두 곱한 후, 전체 데이터의 개수에 대한 제곱근을 구한 것입니다. 기하평균은 주로 비율, 성장률, 등비수열 등에서 사용되며, 큰 값에 민감하지 않아 이상치의 영향을 줄일 수 있습니다.

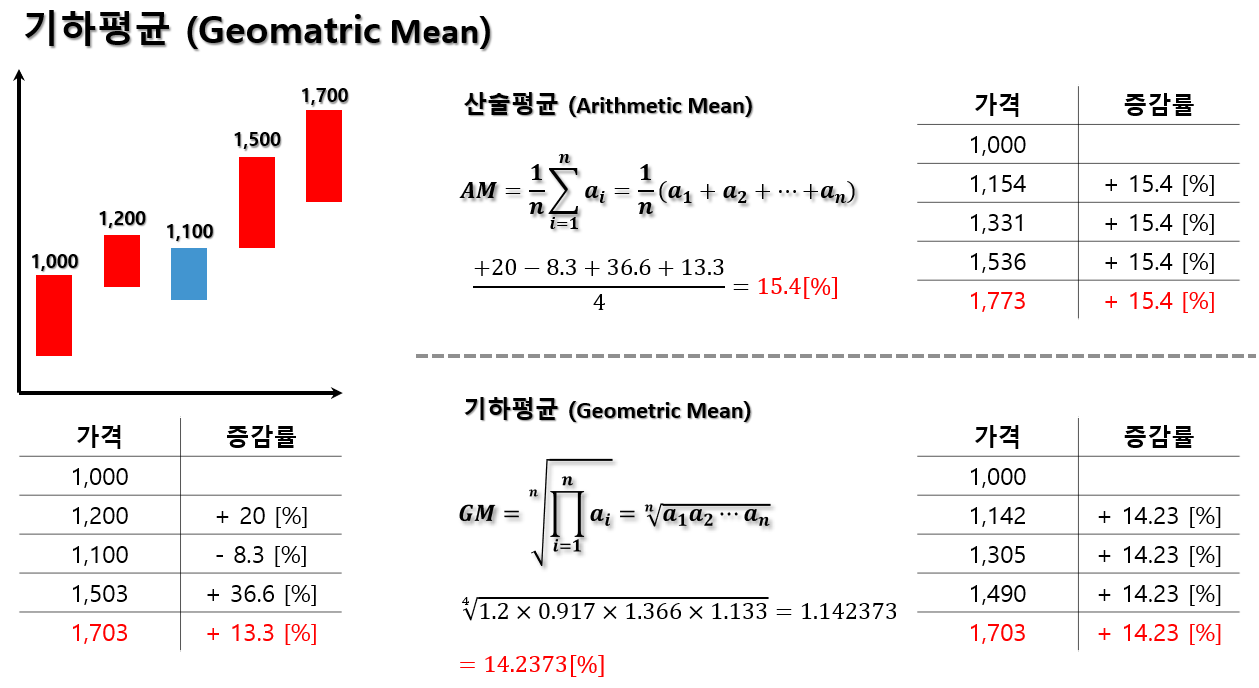
기하평균의 예시를 살펴보겠습니다. 기하평균은 보통 "증가율", "감소율"과 같이 "%"변화율에 따른 평균입니다. 주식의 평균 증감률, 화율의 평균 변동률, 판매량의 평균 증감률이 대표적인 예입니다.
위 예시처럼 주식의 가격이 처음에 1,000원이었으며, 이후 상승과 하락을 반복하여 최종적으로 1,703원이 되었습니다.
만약 이때 증감률을 기존에 사용하던 산술평균에 의해 구하면 평균증감률은 15.4 [%]가 됩니다. 하지만, 실제로 15.4[%] 증가율을 1,000원부터 대입시켜 보면 최종적으로 1,773원이 나오며, 초기 데이터와 오차가 생긴 모습입니다.
이번에는 기하평균을 이용해 평균증감률을 구해 보겠습니다. 기하평균은 증가/감소 량을 모두 곱한 후 데이터의 개수를 1/n승 한 모습입니다. 결과는 평균 증가율이 14.2373 [%]라는 값이 나왔습니다.
이 값을 초기값인 1,000원부터 대입시키면 최종값이 1,703원으로 정확한 값이 나온 것을 확인할 수 있습니다.
3. 조화평균
조화평균은 주어진 데이터 집합의 역수들의 산술평균의 역수로 계산됩니다. 조화평균은 주로 비율이나 속도와 같은 역수 관계를 나타내는 데이터에서 사용됩니다. 작은 값들이 전체 평균에 큰 영향을 미치는 것을 막아주는 특성이 있습니다.
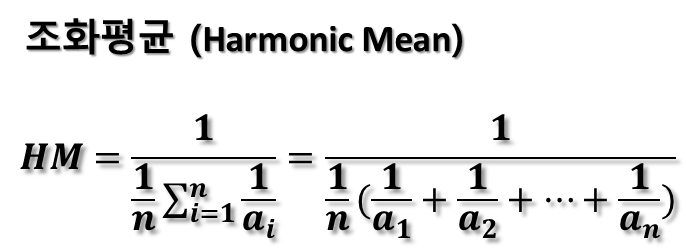
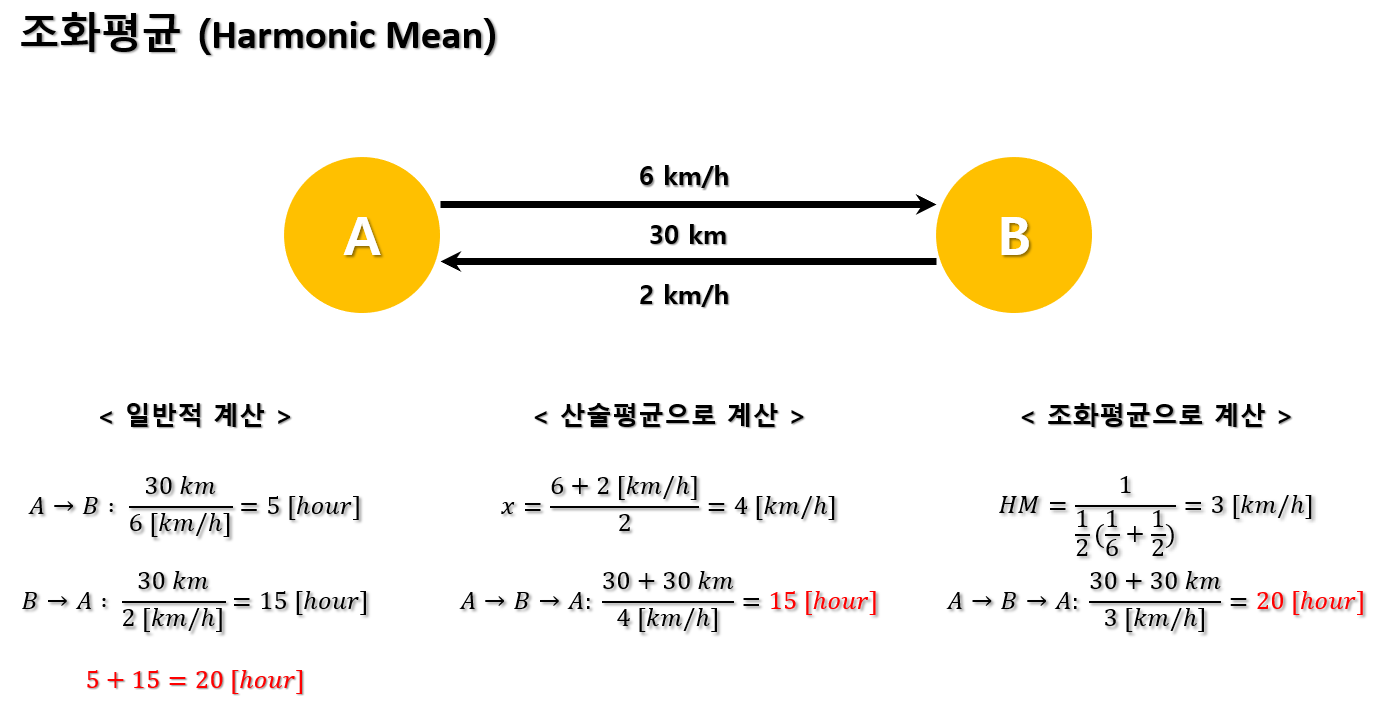
조화평균은 위 예시와 같이 대표적으로 평균 속력을 구할 때 사용 됩니다.
A → B 지점으로 이동할 때는 시속 6km/h의 속력으로 이동하였으며, B → A 지점으로 이동할 때는 시속 2 km/h의 속력으로 이동했습니다. 두 지점 사이의 거리는 30 km입니다.
이 상황에서 두 지점 간의 왕복 시간을 구해 보면 각각 5시간 과 15시간으로 총 20시간이 걸린 것을 확인할 수 있습니다.
만약 평균속력을 구해서 시간을 구해본다면 어떨까요?
일단, 산술평균으로 평균속력을 구해보겠습니다. 6 km/h와 2 km/h의 평균은 4 km/h입니다. 이때 총 이동거리는 왕복이므로 60 km입니다. 이때 속력과 거리를 알고 있으므로 시간을 구해보면 60 [km] / 4 [km/h] = 15시간이 나오므로 정답인 20시간과 오차가 생기게 됩니다.
이번에는 조화평균으로 평균속력을 구해보겠습니다. 조화평균은 각 데이터의 수를 각 데이터의 역수를 더한 것으로 나누어 주면 됩니다. 위와 같이 계산하면 평균 속력은 3 km/h가 나오게 됩니다. 이때 이동시간을 구해보면 20시간이 나오며 정답과 일치하는 것을 볼 수 있습니다.
이렇듯 평균속력을 구할 때는 조화평균을 사용합니다.
4. 가중평균
가중평균은 각 데이터 값에 가중치를 부여하여 계산됩니다. 가중치는 각 데이터의 상대적인 중요성을 나타내며, 큰 가중치가 주어진 값은 전체 평균에 더 큰 영향을 미칩니다. 예를 들어, 학점에 따라 과목별로 가중치를 부여하여 평균을 계산할 때 사용됩니다.
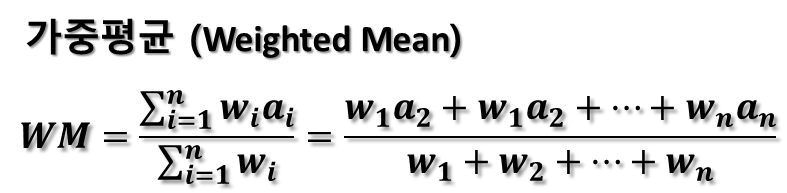
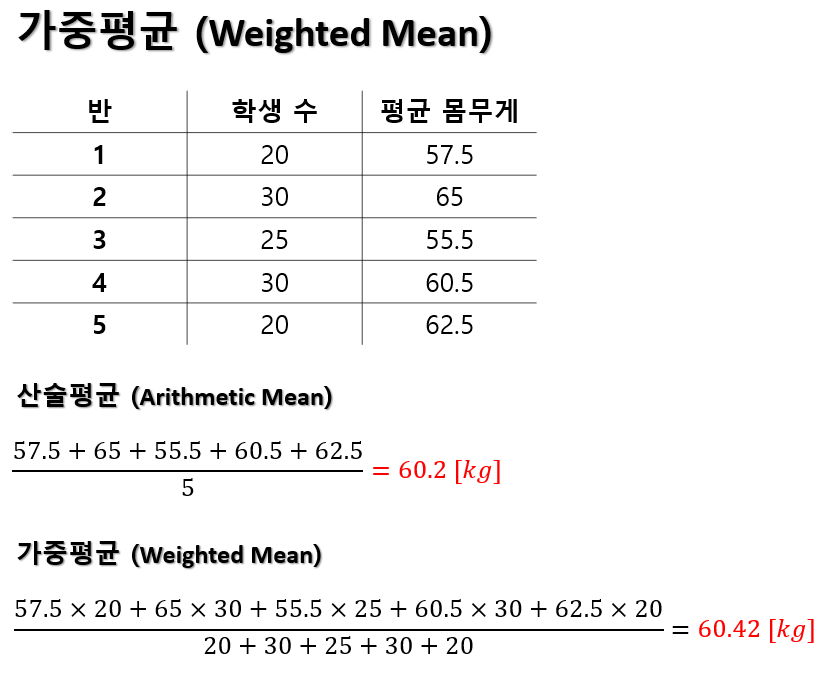
가중평균은 데이터별로 가중치를 다르게 하여 구합니다. 위에 간단한 반 별 평균 몸무게 데이터로 확인해 보겠습니다.
반은 총 5개의 반이 있고, 각각 반 별로 평균 몸무게가 있습니다. 이때 전체 학생수의 평균 몸무게를 구해보겠습니다.
일반적으로 산술평균으로 구 할 경우 반 별 학생수의 차이를 염두하지 않으면 60.2 [kg]의 결과가 나옵니다.
하지만, 각 반 별 학생수를 곱하고 전체 학생수로 평균을 구할 경우 60.42 [kg]의 결과가 나옵니다.
위는 이해를 쉽게 돕기 위한 간단한 예시이며, 실제 생활이나, 실무에서는 적용하는 가중치가 다르며, 훨씬 더 복잡합니다.
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [통계공부] 11.공분산 및 피어슨 상관계수 기본 개념 (공분산 공식) (0) | 2024.01.22 |
|---|---|
| [통계공부] 10. 왜도 및 첨도에 대해 알아보기(왜도, 첨도 공식) (0) | 2024.01.21 |
| [통계공부] 8. 기초통계량의 종류(중심경향성, 퍼짐정도, 왜도, 첨도) (0) | 2023.11.14 |
| [통계공부] 7. 기술통계와 추론통계의 이해와 차이점 (0) | 2023.11.13 |
| [통계공부] 6. 모집단, 표본집단 그래프로 이해하기(예시문제) (0) | 2023.10.30 |




