1. 이항분포란? 이진 결과의 확률분포
이항분포는 이진(binary) 결과를 가지는 실험에서 성공과 실패의 확률을 나타내는 확률분포로, 각 시행이 서로 독립적이고 동일한 확률로 성공 또는 실패하는 경우에 사용됩니다.
이항분포는 대표적으로 주사위를 던지는 행위, 동전을 던지는 행위 등과 같이 각각의 시행이 독립적이며 이진 결과를 갖는 실험을 모형화하는 데 사용됩니다.
2. 이항분포의 공식
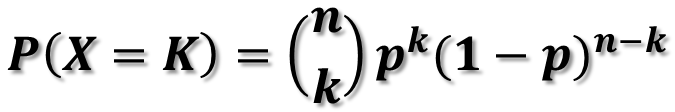

3. 이항분포 엑셀 및 예제로 알아보기
엑셀에서 이항분포는 BINOM.DIST라는 함수를 사용합니다.
BINOM.DIST(Number_s, Trials, Probablility_s, Cumulative)로 구성되어 있습니다.
Number_s : trials만큼의 시행 중 성공할 횟수입니다.
Tials : 독립적 시행 횟수 입니다.
Probablility_s : 각 시행에서 성공할 확률입니다.
Cumulative : TRUE(누적분포 함수), FALSE(확률분포함수)


간단한 동전 던지기를 통해 알아본 이항분포 모습입니다. 한 번에 동전을 10번 던지는 행위를 10번 반복했을 때, 앞면이 얼마나 나오는지에 대한 확률분포입니다. n=10으로 설정, p는 50% 확률인 0.5로 설정했습니다.
10개의 동전을 10번 던질 경우 직감적으로 예상할 수 있듯이, 정규분포와 비슷한 종 모양의 형태가 나왔습니다.
양 끝인, 0과 10 즉, 동전 10개를 한 번에 던졌을 때 모두 다 뒷면이 나올 확률, 모두다 앞면이 나올 확률이 가장 낮으며
10개 중 5개의 동전에서 앞면이 나올 확률이 가장 높은 것을 확인할 수 있습니다.
이항분포의 평균은 5이며, 분산은 2.5입니다.
4. 이항분포와 정규분포의 비교
이항분포와 정규분포를 비교하기 위해 몇 가지의 조건을 추가했습니다.
1. 이항분포의 확률은 0.5로 동일한 상태에서 실행 횟수를 100번으로 증가시켰습니다.
2. Z(표준화 과정)를 통해 이항분포의 X축 값을 -10부터 10까지 범위 안에 넣었습니다.
3. -10부터 10까지 범위를 갖는 표준정규분포 테이블을 생성했습니다.


표준화 과정을 거친 이항분포와 표준정규분포를 한 그래프 안에 표현한 모습입니다. 이항분포가 표준정규분포와 비슷하게 종 모양을 한 것을 확인할 수 있습니다. 하지만, 스케일 차이 때문에 괴리감이 있어 보입니다.
아래에서는 이를 보정하고자 누적분포 함수를 통해, 두 그래프를 합쳐 봤습니다.
이항분포 및 정규분포 엑셀 함수에서 "Cumulative" 값을 True로 변경했습니다.

이항분포 함수와 표준정규분포 함수를 누적분포 형태로 변경하니, 스케일 차이가 없어지고, 둘이 같은 선상에 놓인 모습을 볼 수 있습니다.
그렇다면, 왜 이런 양상이 나타나는지는 "중심극한 정리"를 통해 알아보겠습니다.
2024.01.27 - [통계공부] - [통계공부] 14. 중심극한정리란? 엑셀로 알아보는 중심극한정리(엑셀 파일 첨부)
[통계공부] 14. 중심극한정리란? 엑셀로 알아보는 중심극한정리(엑셀 파일 첨부)
1. 중심극한정리란? 중심극한정리(Central Limit Theorem, CLT)는 통계학에서 주요한 이론 중 하나로, 확률 변수들의 합 또는 평균이 정규 분포에 근사하는 현상을 설명합니다. 이는 다양한 통계적 추론
informyun.com
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [데이터 시각화] Spotfire로 데이터 시각화 해보기 - 상관계수와 결정계수 이론 살펴보기 (0) | 2024.08.22 |
|---|---|
| [통계공부] 14. 중심극한정리란? 엑셀로 알아보는 중심극한정리(엑셀 파일 첨부) (1) | 2024.01.27 |
| [통계공부] 12. 엑셀수식으로 알아보는 정규분포 및 t-분포 (0) | 2024.01.23 |
| [통계공부] 11.공분산 및 피어슨 상관계수 기본 개념 (공분산 공식) (0) | 2024.01.22 |
| [통계공부] 10. 왜도 및 첨도에 대해 알아보기(왜도, 첨도 공식) (0) | 2024.01.21 |




