1. 중심극한정리란?
중심극한정리(Central Limit Theorem, CLT)는 통계학에서 주요한 이론 중 하나로, 확률 변수들의 합 또는 평균이 정규 분포에 근사하는 현상을 설명합니다. 이는 다양한 통계적 추론과 가설 검정에 적용되며, 대표적으로 대표집단의 평균 추정, 가설 검정, 신뢰구간 등에 활용됩니다.
동전 던지기를 예시로 들어보면, 동전을 여러 번 던질 때 앞면이 나오는 횟수의 합 또는 평균은 정규 분포에 근사합니다. 충분히 큰 표본 크기를 가진 경우, 동전 던지기 결과의 평균은 정규 분포를 따를 것이며, 이는 통계적 추론에서 다양한 활용을 가능케 합니다.
2024.01.24 - [통계공부] - [통계공부] 13. 이항분포란? 이항분포의 공식과 정규분포와의 관계
[통계공부] 13. 이항분포란? 이항분포의 공식과 정규분포와의 관계
1. 이항분포란? 이진 결과의 확률분포 이항분포는 이진(binary) 결과를 가지는 실험에서 성공과 실패의 확률을 나타내는 확률분포로, 각 시행이 서로 독립적이고 동일한 확률로 성공 또는 실패하
informyun.com
중심극한정리는 다양한 분야에서 통계적 추론을 할 때 활용됩니다. 특히 대표집단의 평균 추정이나 가설 검정에서 표본 평균의 분포를 정규 분포로 가정하는 기본적인 원리로 사용됩니다.
2. 중심극한정리 성립 조건
중심극한정리는 세 가지 주요 조건 아래에서 성립합니다.
첫째, 독립성(Independence)으로써 확률 변수들은 서로 독립적이어야 하며,
둘째, 동일한 분포(Identically Distributed)로써 동일한 확률 분포를 가져야 합니다.
마지막으로, 대수의 법칙(Law of Large Numbers)은 표본의 크기가 커질수록 표본 평균이 모평균에 수렴한다는 원리를 나타냅니다.
3. 중심극한정리 엑셀로 표현
엑셀에서 =RAND()라는 함수를 이용해 0과 1 사이의 난수를 생성하여 분포를 나타내봤습니다.
총 10회를 진행하였으며, 1회당 1만번의 난수를 생성했습니다.

아래 그래프는 1회 진행시 0과 1 사이의 난수 분포도입니다. 균일하게 분포되어 있는 것을 확인할 수 있습니다.
1부터 10회까지 모두 비슷한 양상을 보입니다.
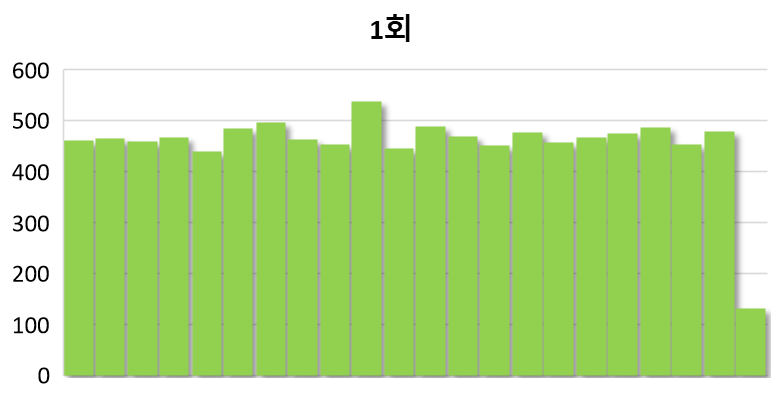
하지만, 1회부터 10회까지의 결과값을 평균으로 구한 뒤, 그래프를 그리면 정규분포와 비슷한 모양이 나옵니다.
아래는 100회, 500회, 1000회, 5000회 까지의 평균의 분포를 나타낸 모습입니다. 100회에서 5000회로 갈수록 정규분포에 가까운 모습을 보입니다.
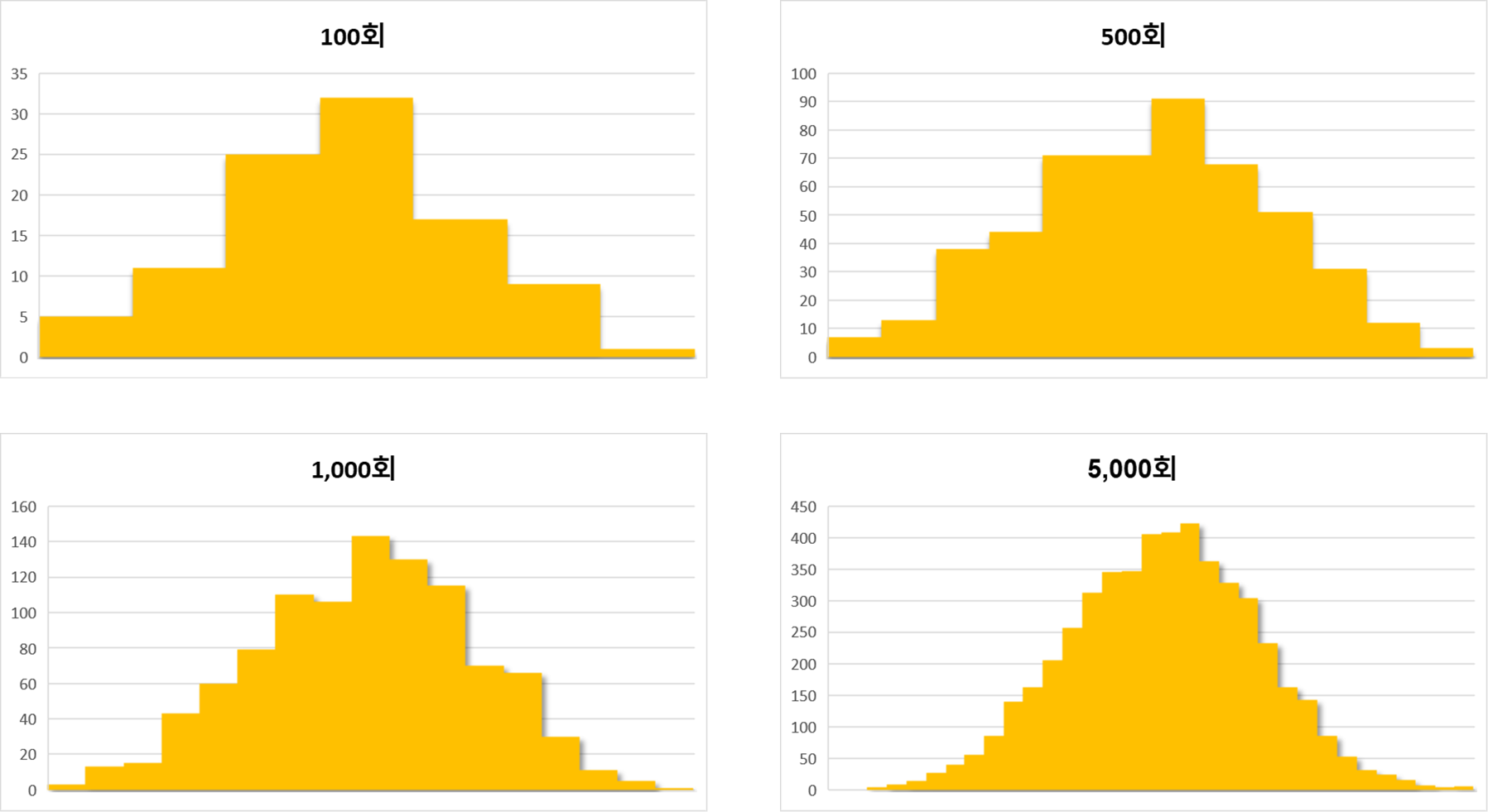
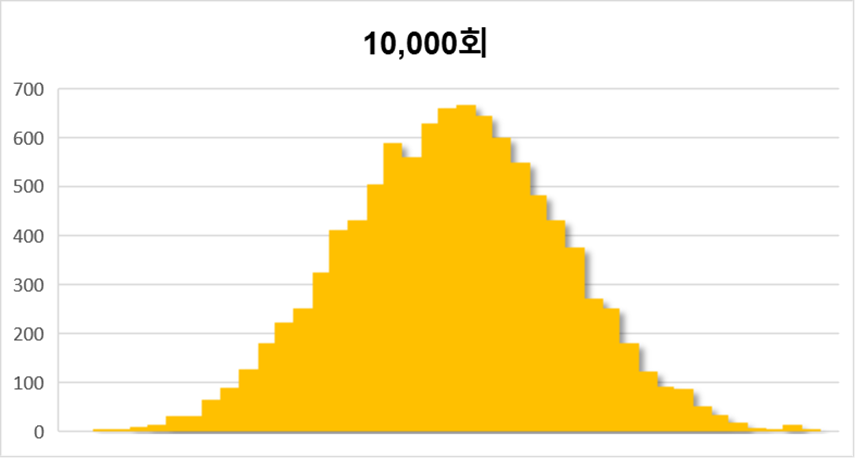
아래는 1회부터 10회까지의 데이터 평균의 분포입니다. 5000회 보다 조금더 정규분포에 가까운 모습입니다.
이 처럼 표본의 크기가 커질수록, 정규분포에 가까워 지는 모습을 볼 수 있습니다. 이는 이항분포에서도 동일합니다.
왜 표본의 크기가 커질수록 정규분포에 가까워지는지, 즉 중심극한정리 공식에 관한 내용은 아래 블로그에서 수식을 풀어 설명해주고 있습니다.
https://blog.naver.com/mykepzzang/220851280035
'데이터 공부 > 통계 공부' 카테고리의 다른 글
| [데이터 시각화] Spotfire로 데이터 시각화 해보기 - F-검정이란?, F-검정과 P-value의 관계 (0) | 2024.08.23 |
|---|---|
| [데이터 시각화] Spotfire로 데이터 시각화 해보기 - 상관계수와 결정계수 이론 살펴보기 (0) | 2024.08.22 |
| [통계공부] 13. 이항분포란? 이항분포의 공식과 정규분포와의 관계 (0) | 2024.01.24 |
| [통계공부] 12. 엑셀수식으로 알아보는 정규분포 및 t-분포 (0) | 2024.01.23 |
| [통계공부] 11.공분산 및 피어슨 상관계수 기본 개념 (공분산 공식) (0) | 2024.01.22 |




