1. 선형회귀(Linear Refression)란?
머신 러닝의 주요 목적은 실제 데이터를 기반으로 모델을 생성하여 다른 입력 값에 대한 출력을 예측하는 것입니다. 그중에서도 가장 직관적이고 간단한 모델은 선형 모델입니다. 예를 들어, 광고 비용과 판매량 데이터를 사용하여 광고 비용으로부터 예상되는 판매량을 예측할 수 있습니다.
선형 회귀는 근사치이지만 최대한 가깝게 데이터를 추정하는 데 의의가 있습니다. 선형 회귀는 수학에서 배운 직선 그래프와 관련이 있으며, 기울기와 절편에 따라 선의 모양이 결정되어 입력 값을 통해 출력 값을 예측할 수 있습니다. 선형 회귀 분석의 목적은 주어진 데이터를 가장 잘 설명할 수 있는 최적의 기울기와 절편을 얻는 것입니다.
1.1. 단순 선형회귀란?
아래 수식처럼 독립 변수 x와 기울기(or 가중치), 편향(bias)로 구성되어 있습니다.
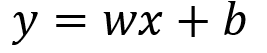
1.2. 다중 선형회귀란?
변수 x가 2개 이상으로 구성되어 있습니다.
이번 블로그에서는 단순 선형 회귀분석 먼저 다루어 보도록 하겠습니다.

2. 단순성형회귀 분석 예제
2.1. 가설 설정
아래 표와 그래프를 보면 공부시간과 점수에 비례하는 가설을 설정했다. 지금부터 이 점들의 상관관계를 가장 잘 나타낼 수 있는 직선을 찾아보도록 하겠습니다.
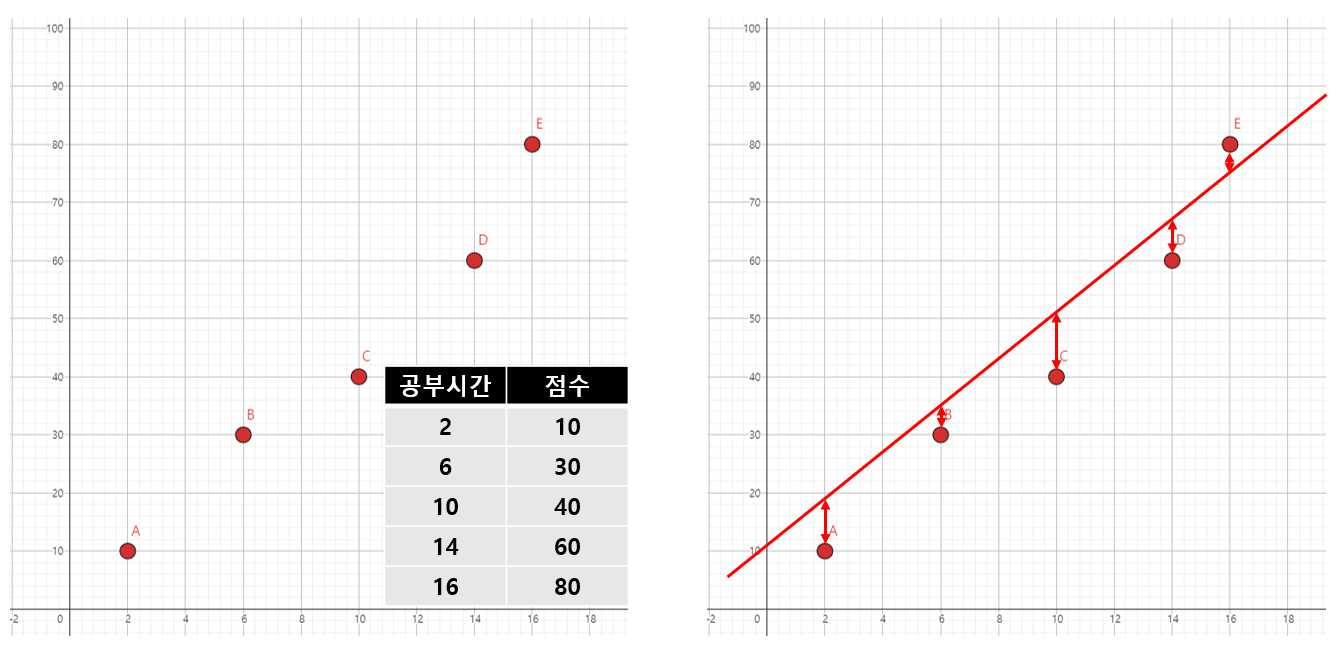
오른쪽 그래프를 보면 본인이 임의로 만든 직선이다. 얼핏 보기에는 해당 점들의 상관관계를 잘 나타내주는 것 처럼 보인다. 하지만 실제로는 이것이 최선이 아니기에 비용함수(Cost Function)의 평균 제곱 오차(Mean Squared Error : MSE)를 이용해 정답을 찾아보도록 하겠습니다.

위에 표에서보면 오차값을 구할 때, 실제값에서 예측값을 빼다 보니 결과가 음수인 경우도 있고 양수인 경우도 있다. 이 점을 보완하기 위해 오차값에 제곱을 해주어, 절대거리로 표현될 수 있도록 합니다. 해당 내용을 수식으로 나타내면 아래와 같습니다.
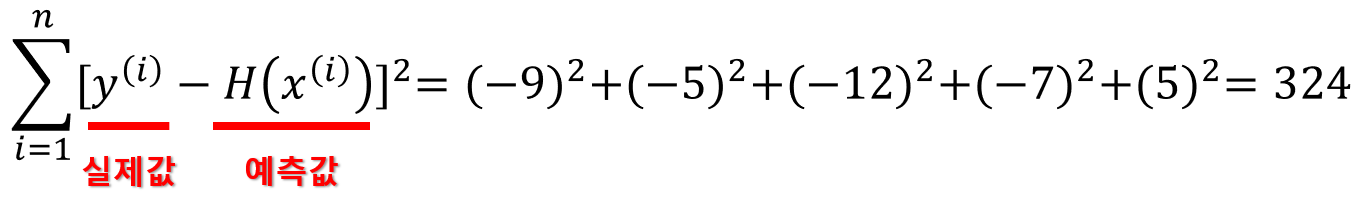

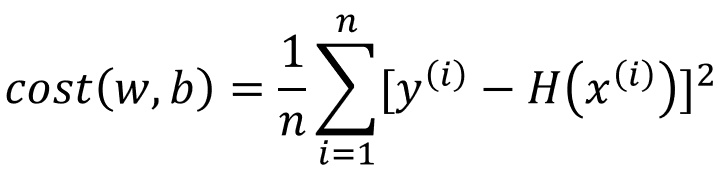
즉, 이 오차값을 비교하여 가장 오차가 작아지게 만드는w(기울기, 가중치)와 b(편향, y절편)을 구하면, y와 x의 관계를 가장 잘 나타내는 직선(Linear)을 그릴 수 있습니다.
이러한 최적화 알고리즘의 기본인 경사하강법은 다음 포스팅에서 다루어 보도록 하겠습니다.
